4. Regression IV
Going Multivariate (Multiple Least-Squares Regression)
The analysis of relationships between two variables is highly useful, and very well understood. As we have seen, there are a plethora of models that can be applied in such instances. These emphasize different aspects of that relationship and provide us with the ability to test quite detailed and specific hypotheses. But the world is complex and, in most cases, we are interested in comparisons that can’t be captured adequately using just two variables. Accordingly, analogues of the methods we’ve discussed so far have been developed to analyze relations between suites of variables. Because these suites are composed of multiple variables—as opposed to pairs of variables—the family of methods we’re now going to discuss are useful for ‘multiple variable’ or ‘multivariate’ analysis (Fig. 1).
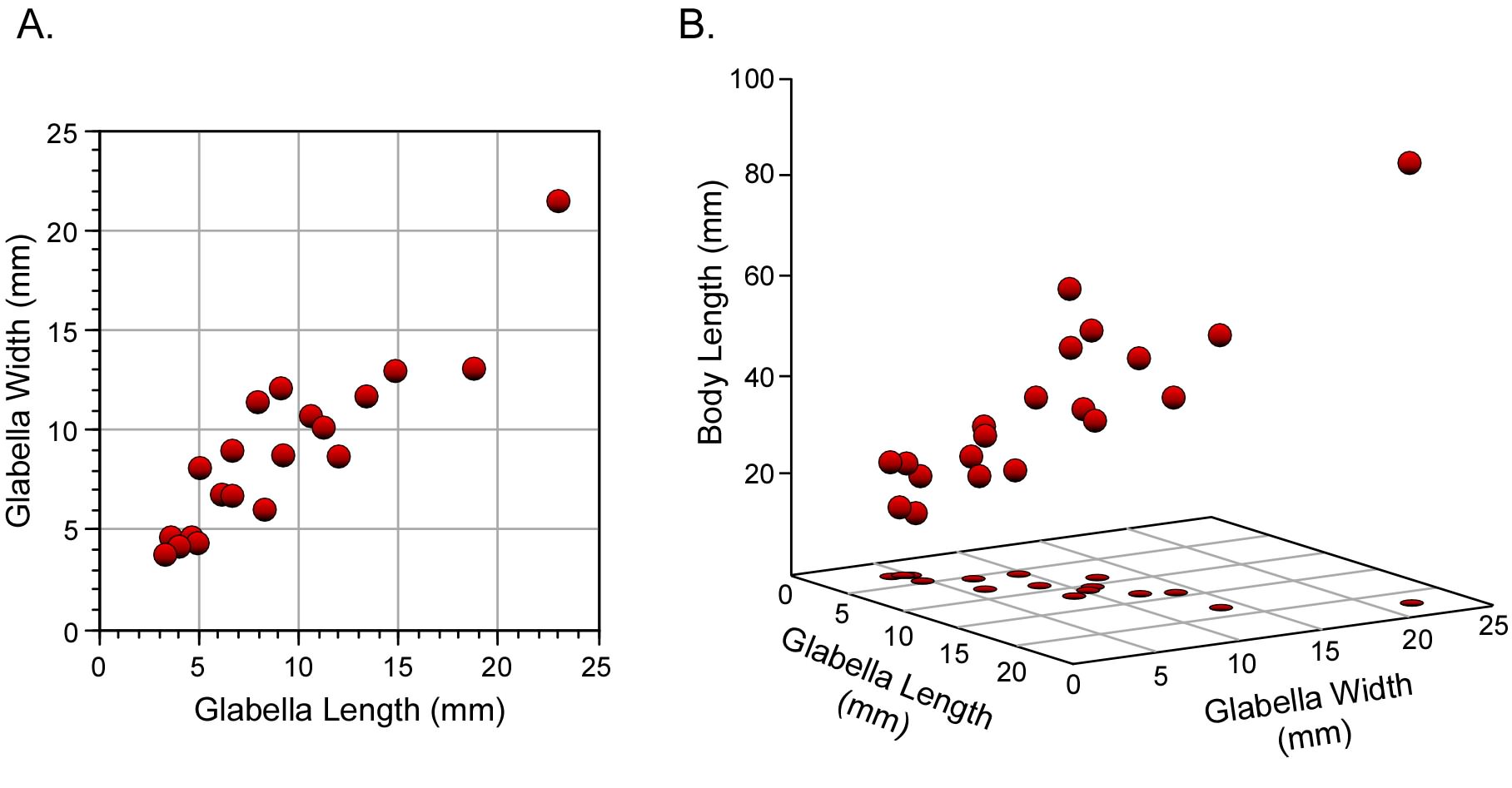
Figure 1. Geometric concepts of bivariate (A) and multivariate (B) datasets. In multivariate data analysis it is commonplace to synonymize variables in the analysis with dimensions in a coordinate system. However, this equation between variables and dimensions is implicit in bivariate analyses as well.
Multivariate methods represent a mathematical bestiary of different approaches, many of which have little in common with others. A natural taxonomy of such approaches that emphasizes underlying similarities would be useful for students and those new to the field. Conceptual differences among the various multivariate methods, however, are such that a formal taxonomy is difficult to justify objectively. Nevertheless, I’ve come to regard the most effective informal taxonomy as tripartite. For the purposes of this column then, we’ll consider the universe of multivariate methods to be composed of ‘the good’, ‘the bad’, and ‘the ugly’. This time out we’re going to focus on ‘the good’. Subsequent columns will take up ‘the bad’ (a series of columns) and ‘the ugly’ (also a series)
So, what do I include in ‘the good’ and what’s so good about them? This category includes all multivariate methods based on the least-squares model. Least-squares methods are ‘good’ because they are grounded on well-established theory and support simple, yet powerful hypothesis tests that are often quite robust to deviations from model assumptions. You may recall we first discussed least-squares in the very first column in this series (Regression 1). Least-squares methods subdivide the variable suite into dependent and independent groupings and seek to express patterns in the former in terms of the latter according to the rule that the sum of the squared deviations of the dependent variable from the model must be minimized.
As always with least-squared methods, the distinction between the dependent variable (usually there’s just one) and the independent variables is critical. Problems appropriate for least-squares analysis involve situations in which you’re trying to estimate one parameter, but only have routine access to another, or a set of others. Since palaeontologists often need to perform just this sort of interpretive feat it’s always been something of a mystery to me why one doesn’t run across more examples of the application of multivariate least-squares methods in the palaeontological literature. This may be changing, however, in that geometric morphometrics has recently embraced the method we’re going to be discussing today as part of its general-purpose, data-analysis toolkit.
| Genus | Body Length (mm) | Glabellar Length (mm) | Glabellar Width (mm) |
|---|---|---|---|
| Acaste | 23.14 | 3.50 | 3.77 |
| Balizoma | 14.32 | 3.97 | 4.08 |
| Calymene | 51.69 | 10.91 | 10.72 |
| Ceraurus | 21.15 | 4.90 | 4.69 |
| Cheirurus | 31.74 | 9.33 | 12.11 |
| Cybantyx | 26.81 | 11.35 | 10.10 |
| Cybeloides | 25.13 | 6.39 | 6.81 |
| Dalmanites | 32.93 | 8.46 | 6.08 |
| Delphion | 21.81 | 6.92 | 9.01 |
| Ormathops | 13.88 | 5.03 | 4.34 |
| Phacopdina | 21.43 | 7.03 | 6.79 |
| Phacops | 27.23 | 5.30 | 8.19 |
| Placopoaria | 38.15 | 9.40 | 8.71 |
| Pricyclopyge | 40.11 | 14.98 | 12.98 |
| Ptychoparia | 62.17 | 12.25 | 8.71 |
| Rhenops | 55.94 | 19.00 | 13.10 |
| Sphaerexochus | 23.31 | 3,84 | 4.60 |
| Toxochasmops | 46.12 | 8.15 | 11.42 |
| Trimerus | 89.43 | 23.18 | 21.52 |
| Zacanthoides | 47.89 | 13.56 | 11.78 |
| Mean | 36.22 | 9.37 | 8.98 |
| Std. Deviation | 18.63 | 5.23 | 4.27 |
Before we begin our discussion proper, let’s set up a small dataset and a hypothetical problem we can use to illustrate the calculations. Our previous data are not well suited to the task of illustrating multivariate procedures in that they are bivariate data. We need more variables. So, let us add the overall length of the carapace to our glabellar measurements (Table 1). As for our problem, under many preservational conditions it is somewhat unusual to recover an entire trilobite. Isolated cephalons are much more common. There is a general relation between size of the cephalon and size of the carapace, but it would be useful to be able to estimate body size from measurements taken on the cephalon. It would also be useful to know which single cephalon measurement constitute the best overall size proxy.
The questions I’ve just posed can be answered by using the multivariate extension of least-squares regression analysis. This method is usually referred to as multiple regression analysis, as if it was the only form of multivariate regression. As we have seen in our discussion of bivariate regression, such is not the case. We’ll return to this nomenclatural issue in a subsequent essay. For now, we’ll test also the statistical significance of the multiple linear regression using a multivariate extension of the analysis of variance (ANOVA) method we discussed last time (see Regression 3 essay in this series).
The basic equation for a multiple least-squares regression is as follows.
(4.1) yi=m1x1i+m2x2i+⋯+mkxki+b+εi
Let’s start by considering the very first regression result we obtained for our example trilobite data from the first essay in this series (see Regression 1 and the Regression 1 worksheet). In that first analysis we used the standard least-squares error-minimization model to estimate the following linear relation between glabellar length (x) and glabellar width (y) that minimized deviation in the latter.
In this expression y represents the dependent variable, m represents the set of partial regression slopes, x represents the set of independent variables (1 through k), b represents the y-intercept, and ε represents the error. In essence, this is the same equation we used for a linear regression, but one that has been expanded to encompass more than a single independent variable. As with bivariate linear regression, the point of multiple regression is to find the set of partial regression slopes that minimize deviation from regression model. Once these have been determined the y-intercept and error terms are easily calculated.
It’s always a good idea to keep a geometric model of what the equations represent in mind when performing numerical analyses. If you understand what the equations look like when graphed you can gain an important sense of intuition about both the analytic method and about the particular dataset under study. Many, if not most, mathematicians gain this sense from innate interest and long years of practice; so much so that the graphics are usually left out of most technical math articles. That’s one of the things that makes them so difficult for non-mathematicians to understand. After all, the equation implies the graph so what’s the point in showing the graph to an audience of professional mathematicians? The point, obviously, is that most researchers who would like to understand the math don’t have the facility of professional mathematicians for visualizing the geometric meaning of equations. This is especially important in multivariate studies that might contain large suites of variables. Fortunately, computer graphics packages are included with almost all numerical analysis packages. These tools take the drudgery, time, and expense out of generating the necessary graphics. Learn to use them. They will help you.
It is not a big conceptual leap to see that the (now) familiar y=mx+b linear regression equation represents a straight line usually inclined at some angle to the horizontal and vertical graph axes. Now, what does the y=m1x1+m2x2+b multiple regression model equation look like? That model will have a dependent variable (y) and two independent variables (x1,x2). As we saw in Figure 1, these variables can be portrayed as axes in a three-dimensional coordinate system. The model has two linear slopes, one expresses variation in the x1 vs y plane, and the other in the x2 vs y plane, Combine these into a single three-dimensional coordinate and (I hope) you can see the geometric model for a multiple regression analysis is a plane cutting through a cloud of points (Fig 2). This plane is oriented such that the deviation of the points is minimized along the y-axis. Of course, an infinity of planes with these slopes exist. You can visualize them as a stack of parallel planes above and below the one drawn in Figure 2. The particular plane that best corresponds to these data is located within this system of planes by the y-intercept. This is a single number because the slopes along both the x1y and x2y planes intersect the y-axis at the same point.
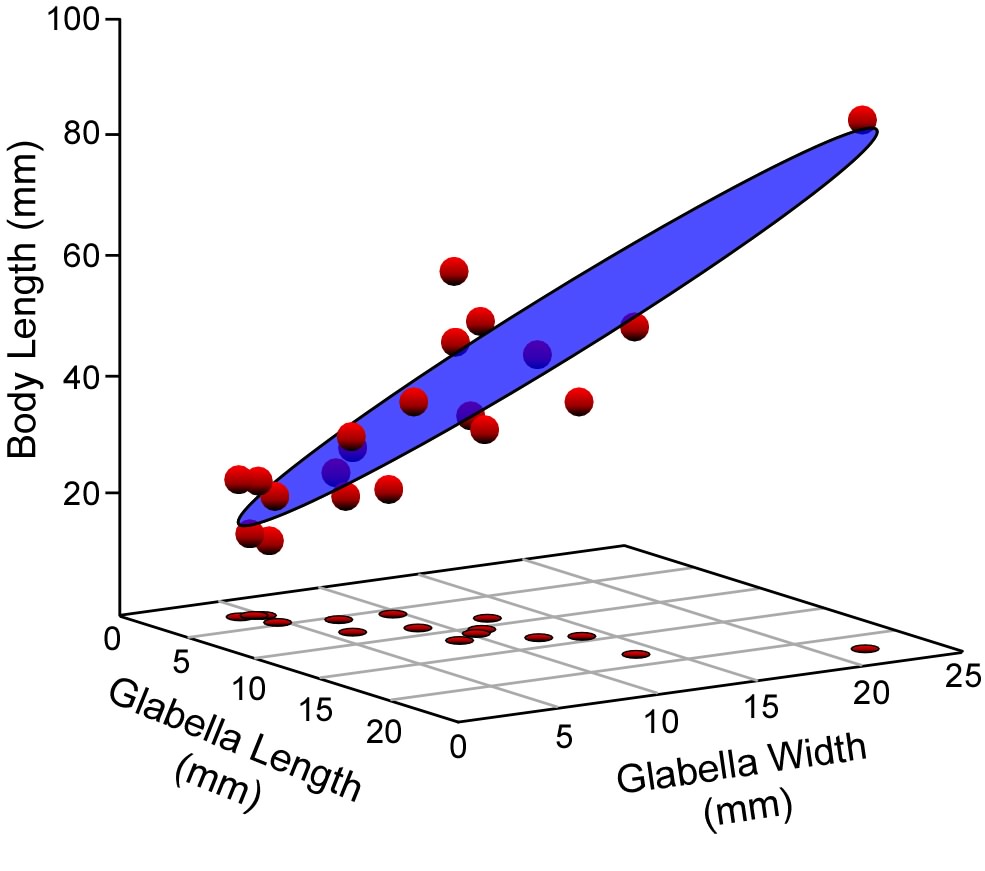
Figure 2. Because multiple linear regression includes more than a single independent variable, the result of an analysis is best visualized as a plane rather than as the line of a bivariate regression analysis. This plane (here shown in the three-dimensional space of a three-variable analysis) is defined by a series o slopes and a y-intercept value, and oriented such that deviations between the observed data points and the plane are minimized in the direction of the dependent variable (the vertical, or z-axis of this diagram).
Essentially what we need to do is solve a set of simultaneous equations, one equation for each set of observations or measurements in our system. How to do this? Say I wanted to find values of x1 and x2 such that the following relations were fulfilled.
2x1=4x2=19
5x1+15x2=55
The way most people would approach this problem would be to re-express these relations in their matrix form, as follows.
(4.2) AX=B
In this expression A is the matrix of variable coefficients or weights, X is the matrix of unknown values, and B is the matrix of results. Expanding this symbolic form using our example values Equation 4.2 becomes …
(4.3) [25515]×[x1x2]=[1955]
To solve this equation we must use simple matrix algebra to isolate the unknowns on one side of the equals sign so they can be expressed in term of known quantities. Thus, we must multiply both sides of the equation by the inverse of the A matrix.
(4.4) A−1AX=A−1B
ince the product of A-1A is the identity matrix (I), and since the product of I with any matrix is that matrix, Equation 4.4 simplifies to …
(4.5) X=A−1B
Thus, pre-multiplying the matrix of resulting values with the inverse of the matrix of variable coefficients will gives us the values of the coefficients that satisfy the expressions.
[x1x2]=[3−1−10.4]×[1955]
[x1x2]=[23]
Matrix inversion and multiplication are labour-intensive processes if you try to do the arithmetic with a hand calculator, much less by hand. Fortunately, MS-Excel includes matrix inversion and matrix multiplication in its suite of functions (as MINVERSE and MMULT, respectively). One does need to be careful in that these operations can result in the generation of very large numbers that can be rendered inaccurate by truncation. Provided care is taken to transform inherently large numbers into ‘normal sized’ counterparts and not try to solve too large a system of equations, though, Excel should perform adequately. An example of these calculations is provided in this essay’s Palaeo-math 101 worksheet.
OK. So solving matrix equations in Excel is pretty neat. What does it have to do with multiple regression? Well, the equations that need to be solved in a multiple regression problem can be expressed—and solved—in exactly the same way. Take our trilobite data, for example: one dependent variable (Body Length) and two independent variables (Glabella Length and Glabella Width) all linked together by a set of constant values (slopes) representing the coefficient weights of the example problem above. The only real difference is that, whereas we only had two equations in the matrix-algebra example, our trilobite data are composed of twenty different simultaneous equations, one for each genus. Not only that, we know it is exceedingly unlikely all the equations will be able to be satisfied perfectly by a unique two-coefficient solution. The best we can do is estimate the general relation between our variables and use those to fit the best model we can, subject, of course to the standard least-squares constraint.
Once we understand the logic of this basic approach we’re almost there. The only piece of the puzzle we don’t yet have is a way to estimate the general relation between variables. Actually, we discussed one way of approaching this estimation in the Regression 2 essay when I explained the concept of covariance. At that time, we needed a way of estimating the relation between glabellar width and length in order to calculate the major-axis regression. As you will recall from that essay, the covariance is a measure of the proportion of variance the two variables have in common. This time out we need a similar quantity, but it is computationally convenient not to base this estimate on the variables’ raw values, but on their standardized equivalents (see Regression 2 for a discussion of data standardization).
The correlation coefficient is determined by normalizing the covariance calculated between two variables by the product of those variables’ standard deviations.
(4.6) r12=COV12s1s2
This is a dimensionless number that expresses the co-linearity of the variables irrespective of differences in their magnitude. Correlations of 1.0 signify perfect co-linearity (most often seen when a variable is correlated with itself). Correlations of -1.0 signify perfect negative co-linearity (rarely seen in observed data). Correlations of 0.0 signify perfect independence. Between these extremes lie a large range of values. The correlation coefficient is used to express the degree to which real observations approximate these end-member conditions.
Structural relations among the variables can be quantified in a correlation matrix that represents all pairwise comparisons between all variables. The correlation matrix for the three variable shown in Table 1 is shown as Table 2.
| y (BL) | x1 (GL) | x2 (GW) | |
|---|---|---|---|
| y (BL) | 1.000 | 0.895 | 0.859 |
| x1 (GL) | 0.895 | 1.000 | 0.909 |
| x2 (GW) | 0.859 | 0.909 | 1.000 |
There are several things to note about this matrix. First, values along the left-right diagonal—also known as the ‘trace—are all 1.000 because these are positions within the matrix representing the correlation of a variable with itself. It should also be evident that the correlation matrix is ‘square’ in the sense that the upper-right triangle of values (above the diagonal trace of perfect correlations) is the mirror image of the lower-left triangle. Finally, note that, for our data, all the variables appear to have sub-equal, high correlations with one another. This is typical for correlations between morphometric measurements.
The correlation matrix embodies all the information we need to solve our multiple correlation problem. In this simple example, the simultaneous equations we need to solve are as follows.
1.000M1+0.909M2=0.895
0.909M1+1.000M2=0.895
As in the example above, these equations are in the form AX=B, and can be expressed in matrix form this way.
[1.0000.9090.9091.000]×[x1x2]=[0.8950.859]
By taking the inverse of A matrix, and rearranging the matrix equation algebraically, we obtain the following relation.
[x1x2]=[5.767−5.244−5.2445.767]×[0.8950.859]
Finally, carrying out the matrix multiplication we find …
[x1x2]=[0.6580.262]
These are the partial regression coefficients for the original data in their standardized form. Not only do they satisfy the equations above2, they represent the slopes of the partial regression of x1 on y and x2 on y, respectively.
At this point let’s be clear what we mean by partial regression. These values represent the average change (in standard deviation units) of the dependent variable (y) for a unit change in each of the independent variables (x) in isolation, the other being kept constant. Because these coefficients are set to the same (unitless) scale, they can be compared with one another directly. Thus, our analysis indicates Glabella Length is a stronger proxy for Body Length than Glabella Width.
Because the data in Table 1 are presented in units of millimetres, not standard deviations, we cannot use the standardized form of the partial regression coefficients to calculate the model values. Fortunately, the scalings needed to transform the values to their unstandardized, or conventional unit equivalents are very simple, amounting to nothing more than multiplying them by the ratio of the standard deviations of the dependent and independent variables.
(4.7) mY⋅Xk=m′Y⋅Xk(SYSXk)
When these calculations are carried out for the trilobite data the m1 and m2 coefficients become 2.342 and 1.140 respectively. Once these have been obtained the value of the y-intercept can be determined in the normal manner …
(4.8) b=¯y−(my⋅x1¯x1)−(my⋅x2¯x2)
… yielding the following multiple regression.
(4.9) yi=2.342xi1i+1.140x2i+4.029+εi
This equation can be used as a general expression for estimating body length from glabellar length and width. The next obvious questions are: (1) how well does this regression perform and (2) is the regression statistically significant? The concepts and techniques used to answer these questions for simple linear regression were developed in the last essay (Regression 3). Fortunately, these have straight-forward analogues in multiple linear regression. The most useful single indicator of regression quality is, once again, the coefficient of determination, which, for a multiple regression, is termed the coefficient of multiple determination and calculated as follows.
(4.10) R2=K∑k=1ry⋅km1y⋅xk
In this expression K represents the number of independent variables.
Thus, for our trilobite regression R2=((0.895)(0.658))+((0.859)(0.262)), or r2=0.814, This is quite a good result, indicating that the regression accounts for or explains over 80 per cent of the observed variation in the dependent variable. That’s not a bad generalized estimator, especially insofar as glabellar length and width, on logical grounds, would seem to be somewhat independent of body length per se. Of course, this result only holds for this particular dataset. Inclusion of a greater variety of trilobite morphologies would, perhaps, yield a result closer to our intuition (or not?). Nevertheless, the principles and utility of the method are clearly demonstrated in this small example.
The statistical significance question is handled by the same ANOVA-based method described in detail last time. This time around, though, I’ll show you are trick that will make the setting up of regression ANOVAs much simpler. Instead of calculating estimated values for the dependent variables and using these to summarize the residual variation about the regression model, we can use the coefficient of multiple determination to calculate the necessary forms of these values directly. First, find the sum of squares of the original dependent variable observations. That value is 32,827.24 mm2. The sum of squares of the estimated y-values and the residual y-values can be calculated directly using the following equations.
(4.11) ∑ˆyi=R2∑Y2i
(4.12) ∑(yi−ˆyi)2=(1−R2)∑y2i
Once these quantities are known the following table can be completed and the relevant F-statistic calculated.
| Source of Variation | Sum of Squares | Degrees of Freedom | Mean Square | F-statistic |
|---|---|---|---|---|
| Total | 32827.24 mm2 | 19 | 1727.75 mm2 | 37.12 |
| Regression | 26710.51 mm2 | 2 | 13335.26 mm2 | |
| Error | 6116.72 mm2 | 17 | 359.81 mm2 |
This is a statistically significant result. Remember, for multiple regression the degrees of freedom due to regression is equivalent to the number of independent variables and that due to the error is one less than the number of data points, less the number of independent variables. All other terms in the ANOVA are calculated as described in the Regression 3 essay.
Multiple regression is a vast topic. Many more tests and procedures exist for determining such things as whether there is a significant difference between partial regression coefficients, standard errors for various regression parameters, significance of individual variables, and so forth. Because multiple linear regression is one of ‘the good’ methods, there are also many sources of information about this technique. The references at the end of this essay will direct you to some useful standard presentations and summaries.
The Paleo-math 101 worksheet that accompanies this essay provides complete Excel calculations for the example discussed above and for an additional example in which the distance between the eyes is included as a third variable in the multiple regression. Comparison of these examples is instructive, especially in terms of seeing how the answer is dependent on the number and character of the variables considered by the analysis.
One final word of caution regarding calculations. Because of the sizes of the numbers generated during a multiple regression analysis, and the complexity of the calculations, most multiple regression problems should be solved using a dedicated computer program or high-level generalized math package (e.g., Mathematica, MatLab). The Excel spreadsheet supplied with this essay will solve small multiple regression problems, but its main purpose is to provide complete illustration of the calculations discussed in the text.
References
Davis, J. C. 2002. Statistics and data analysis in geology (third edition). John Wiley and Sons, New York. 638 pp.
Motulsky, H. 1995. Intuitive biostatistics. Oxford University Press, Oxford. 386 pp.
Sokal, R. R. and Rohlf, F. J. 1995. Biometry: the principles and practice of statistics in biological research (third edition). W. H. Freeman, New York. 887 pp.
Swan, A. R. H. and Sandilands, M. 1995. Introduction to geological data analysis. Blackwell Science, Oxford. 446 pp.
Zar, J. H. 1999. Biostatistical analysis, Fourth Edition. Prentice Hall, Upper Saddle River, New Jersey. 663 pp.
Footnotes
1In order to include additional measurements this dataset differs from those used in previous essays.
2If you check you’ll find the actual values are a little off, but this is due to the fact that I’ve only chosen to show you the answers to three significant figures.
