6. Factor Analysis
Principal components analysis (PCA)-along with its basis method, eigenanalysis-is arguably the workhorse of multivariate analysis. There are multivariate methods that don't employ some aspects of eigenanalysis, but eigenanalysis-based methods easily predominate in terms of both number and application. Therefore, it behoves us to spend some time looking at the variants of PCA, going through their basic calculations, and discussing the context within which their use is justified. In this essay we'll explore factor analysis, a method often regarded as a simple variant of principal components analysis and one that used to be much more popular among palaeontologists than it seems to be today. Along the way we'll gain deeper insight into the mechanics and appropriate use of both methods
In discussing PCA last time, we asked the questions (1) what structural relations exist among our three trilobite variables, (2) whether we could take advantage of these relations to create new variables with more desirable properties and (3) what the ordination of the species in our sample looked like when plotted against our new variables. This time, let's focus on a slightly different question, but one you might have thought we were discussing last time, 'What covariance-based structural relations exist between our three trilobite variables?'. What's the difference between structural relations and covariance-based (or correlation-based) structural relations and, since PCA is (usually) based on the covariance or correlation matrix, didn't we do that last time? It's actually not quite as simple as that. Read on to learn the difference.
As usual, we'll make use of our simple trilobite dataset (Table 1, see also Fig. 1).
| Genus | Body Length (mm) | Glabellar Length (mm) | Glabellar Width (mm) |
|---|---|---|---|
| Acaste | 23.14 | 3.50 | 3.77 |
| Balizoma | 14.32 | 3.97 | 4.08 |
| Calymene | 51.69 | 10.91 | 10.72 |
| Ceraurus | 21.15 | 4.90 | 4.69 |
| Cheirurus | 31.74 | 9.33 | 12.11 |
| Cybantyx | 26.81 | 11.35 | 10.10 |
| Cybeloides | 25.13 | 6.39 | 6.81 |
| Dalmanites | 32.93 | 8.46 | 6.08 |
| Delphion | 21.81 | 6.92 | 9.01 |
| Ormathops | 13.88 | 5.03 | 4.34 |
| Phacopdina | 21.43 | 7.03 | 6.79 |
| Phacops | 27.23 | 5.30 | 8.19 |
| Placopoaria | 38.15 | 9.40 | 8.71 |
| Pricyclopyge | 40.11 | 14.98 | 12.98 |
| Ptychoparia | 62.17 | 12.25 | 8.71 |
| Rhenops | 55.94 | 19.00 | 13.10 |
| Sphaerexochus | 23.31 | 3,84 | 4.60 |
| Toxochasmops | 46.12 | 8.15 | 11.42 |
| Trimerus | 89.43 | 23.18 | 21.52 |
| Zacanthoides | 47.89 | 13.56 | 11.78 |
| Mean | 36.22 | 9.37 | 8.98 |
| Variance | 346.89 | 27.33 | 18.27 |
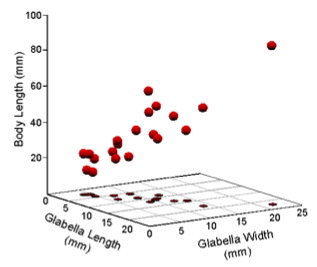
Figure 1. Scatterplot of Table 1 data in a Cartesian coordinate system.
Principal components analysis is used when we want to understand the structure of a set of variables based on a comparison of their variances. Remember, the eigenvalues we extract from a covariance or correlation matrix are ordered in terms of the amount of observed variance they account for. In terms of the covariance or correlation matrix, you can think of PCA as being a method that focuses on reproducing the diagonal or trace of these matrices in the most efficient manner possible. That's a very useful thing to do, as we have seen. But it's not the only thing you can do with a covariance or correlation matrix. The information in the off-diagonal elements is also interesting and useful. More to the point, it's possibly more pertinent to a large range of palaeontological problems than an assessment of the variance structure per se. The information carried in these off-diagonal elements is the realm of factor analysis.
Factor analysis actually has a somewhat nefarious reputation in many quarters due to the nature of its statistical model and due to its overenthusiastic use in the field of psychology; especially the branch of this field that deals with intelligence testing (see Gould 1981). Irrespective of this, in order to understand factor analysis one needs to understand the model on which it is based, and there is no better way to gain this understanding than by going back to the problem factor analysis was originally developed to solve.
Around 1900 Charles Spearman, who was interested in intelligence testing, noticed that the scores on different academic subject tests often exhibited an intriguing regularity. Consider the following correlation matrix of test scores.
| Classics | French | English | Mathematics | Music | |
|---|---|---|---|---|---|
| Classics | 1.00 | 0.83 | 0.78 | 0.70 | 0.63 |
| French | 0.83 | 1.00 | 0.67 | 0.67 | 0.57 |
| English | 0.78 | 0.67 | 1.00 | 0.64 | 0.51 |
| Mathematics | 0.70 | 0.67 | 0.64 | 1.00 | 0.51 |
| Music | 0.63 | 0.57 | 0.51 | 0.51 | 1.00 |
If the effect of the diagonal values are ignored, in many cases the ratio of values between rows of the matrix approximates a constant. Thus, for English and Mathematics...
0.78/0.70=1.114
0.67/0.67=1.00
0.51/0.51=1.00
...and for French and Music...
0.83/0.63=1.317
0.67/0.51=1.314
0.67/0.51=1.314
Spearman proposed these sorts of data had the generalized form.
(6.1) Xi=biF+ei
Where Xi was a standardized score the ith test, F was a 'factor' value for the individual taking the battery of tests, and ei was the part of Xi specific to each test. Because Spearman was dealing with the matrix of correlations, both X and F were standardized, with means of zero and standard deviations of one. This fact was used by Spearman in his other factor analysis insight, that b2i is the proportion of the variance accounted for by the factor (see Manley 1994 for an easy-to-understand proof of this result).
Using these relations Spearman was able to postulate that mental test scores were composed of two parts, one (F) that was common to all tests and so reflected the innate abilities-or the 'general intelligence'-of the test taker, and one (e) that was specific to the test and so could be construed as evidence of either the subject-specific aptitude of the test taker, culture-based bias in the test, or some combination of the two.1
Generalizing the relations presented above it can be appreciated that the model underlying factor analysis has the following form.
(6.2) X1=b11F1+b12F2+⋯+b1jFj+e1X2=b21F1+b22F2+⋯+b2jFj+e2X3=b31F1+b32F2+⋯+b3jFj+e3⋮Xi=bi1F1+bi2F2+⋯+bijFj+ei
Note the similarity between this model and the multiple regression analysis model (see PalaeoMath 101: Part 4 - Regression, Equation 4.1). As Jackson (2003) notes, the creators of factor analysis viewed it originally as a type of multiple regression analysis. But they had a problem. Unlike a standard regression problem in which a set of observations (X) is related to an underlying general model (Y) by specifying a rate of change (the slope m), one cannot observe the factor(s) (F) directly. As a result, their structure must be inferred from the raw data, which represents an unknown mixture of common and unique variance. In essence, you can't use multiple regression to sort this problem out because all quantities on the right-hand side of the equation are unknown.
At this juncture it's important to recognize that principal components analysis (PCA) can't resolve this problem any more than multiple regression analysis can. The PCA model (see PalaeoMath 101: Part 5 - PCA, Eigenanalysis & Regression, Equation 5.1) is simply a transformation that re-expresses the observed data in a form that maximizes variance on the various PC vectors (= axes) and ensures the orientational independence of these vectors from one another. This approach focuses on accounting for variance and keeps extracting vectors until the remaining unaccounted for-or residual-variance is exhausted or drops below some arbitrarily-determined amount. Factor analysis isn't trying to account for the variance exhibited by a sample, but instead focuses on recovering the structure of the covariances among variables as completely as possible. In other words, PCA attempts to reduce the residual values of the diagonal or trace of the covariance or correlation matrix. Factor analysis tries to model the covariances or correlations in such a way as to minimize the residual values of the off-diagonal elements. You should use PCA when you want to test hypotheses about a sample's variance. You should use factor analysis when you want to model or test hypotheses about the structure of relations among variables that have been measured across a sample.
Among the many myths about factor analysis is the idea that it only differs from PCA in the sense that the number of factors extracted from the covariance or correlation matrix in a factor analysis is less than the number of variables whereas, in PCA, the number of components extracted equals the number of variables (e.g., see the discussion of factor analysis in Hammer and Harper 20062). Nothing could be further from the truth. Indeed, one of the principal uses of PCA is to reduce the dimensionality of a dataset from m variables to p components, where p<m. This erroneous view of the relation between PCA and factor analysis has been perpetuated by the innumerable over-generalized and/or superficial descriptions of both techniques that have been published in the technical literature, and especially in the user's guides of multivariate data analysis software packages within which these methods are routinely confused.
There are a number of ways to perform a factor analysis. The method I'll outline here would not be accepted by many as 'true' factor analysis; especially as it is practiced in the social sciences. However, this is a basic version of the procedure most geologists refer to as factor analysis (e.g., Jöreskog et al. 1976; Davis 2002; Swan and Sandilands 1995). It starts with a PCA. If one has reason to suspect the form of an underlying model that implies a specific number of factors, this number can be input and the factor solution computed directly. For Spearman's intelligence test data, he suspected a one-factor solution, the one-factor model quantifying his 'general intelligence' index and the remaining test-specific variation being subsumed into the error term. For our trilobite data (Table 1) we might suspect a priori a two-factor model with one factor representing 'generalized size' and the other 'generalized shape', in which case the error term would represent genus-specific deviation from these generalized indices. It is often the case, however, that one has little idea beforehand how many factors are present in the data.
If you find yourself in the latter situation there is no cause for undue alarm. Factor analysis – like PCA – can be used in an exploratory mode. There are a number of rules-or-thumb for both factor analysis and PCA that can help you decide how many axes to use. If you are working with a correlation matrix, one of the most popular and easiest to remember is to consider only those axes that contain more information than the raw variables. This makes sense in that these axes are easy to identify (all will have eigenvalues > 1.0) and there seems little logical reason to make much of a fuss over composite variables that don't contain as much information as their raw counterparts. An exception to this rule, however, would be an analysis that employed a small number of raw variables. In such cases there won't be much variance to distribute over the axes anyway and a single-variable solution may not be adequate to test your hypothesis. Another popular rule-of thumb is the so-called Scree Test in which the magnitudes of the eigenvalues are plotted in rank order and a decision made on the basis of where the slope of the resulting curve breaks from being dominantly vertical to dominantly horizontal.3 Of course, both these tests can be applied to PCA as well as factor analysis. The other quick and easy test to apply when considering whether factor analysis is appropriate is Spearman's constant proportion test (see above). If a large number of the ratios between the non-diagonal row values of the correlation matrix do approximate a constant, the data exhibit the classic structure assumed by the factor analysis model. If such a structure cannot be demonstrated, factor analysis may proceed, but should be interpreted with caution.
The PCA results for the trilobite data correlation matrix are listed below (see also the R-Mode Factor Analysis worksheet of the PalaeoMath 101 Spreadsheet).
| Eigenvalues | Variance (%) | Cum. Variance (%) |
|---|---|---|
| 2.776 | 92.541 | 92.541 |
| 0.142 | 4.719 | 97.260 |
| 0.082 | 2.740 | 100.00 |
| Variables | PC1 | PC2 | PC3 |
|---|---|---|---|
| Body Length (x1) | 0.573 | 0.757 | -0.314 |
| Glabella Length (x2) | 0.583 | -0.108 | 0.805 |
| Glabella Width (x3) | 0.576 | -0.644 | -0.504 |
If you've read the last column you should be familiar with the interpretation of these tables, but we'll go through it again, just for practice. The overwhelming majority of the variation in these data is being expressed on PC1 (Table 3). On this axis all three variables have subequal positive loadings (Table 4). This is highly suggestive of this axis representing a generalized size index and that size variation represents the predominant component of variation in the dataset. The remaining two PC axes represent much smaller proportions of the observed variance and the alternating signs of their eigenvector loadings indicate they represent axes of localized size (= shape) variation. Here PC2 expresses a contrast between body length and glabellar width variation while PC3 mostly expresses a contrast between glabellar length and linked body length-glabellar width variation.
Since the second eigenvalue expresses less than a third of the total variance (= 3.0) it is tempting to only consider PC1 important. After all, in the raw data each standardized variable contributes 1.0 standard deviation units to the total. However, we're going to include PC2 in our factor analysis solution because (1) we have good reason to suspect these data are composed of a size factor and a shape factor and (2) by doing so we will be considering over 95 percent of the observed sample variance.
Unlike classical PCA, factor analysis scales the factor loadings by the covariance/correlation matrix's eigenvalues. Note in equation 6.2 the place of the a-values in the PCA general equation has been taken by b-values. The change in symbol signals this basic difference in the two loading coefficients. In order to calculate the loadings of a factor analysis the following relation is used.
(6.3) bij=√λiaij
Where bij is the factor loading λi, is the eigenvalue of the jth eigenvector, and aij is the corresponding PCA loading. Using this relation and calculating a solution for the a two-factor model, the equations of the factor axes are as follows.
| Variables | F1 | F2 | Communality |
|---|---|---|---|
| Body Length (x1) | 0.954 | 0.285 | 0.992 |
| Glabella Length (x2) | 0.972 | -0.041 | 0.947 |
| Glabella Width (x3) | 0.959 | -0.242 | 0.079 |
The communality is the sum of the squares of the bij values for each variable. This quantity expresses the proportion of the variance provided by those variables to the model factor(s). The quantity '1- the communality', then, expresses the proportion of the variable's variance attributable to the error term of the factor. As you can see from Table 5, under this two-factor solution all variables exhibit a high communality indicating the residual error is very small.
The communality values are one thing, but we can use a little trick at this point to emphasize the difference between PCA and factor analysis. Another way of calculating the covariance or correlation matrix is to multiply the matrix of raw measurements (or standardized raw measurements, in the case of the correlation matrix) by the transpose4 of that same matrix.
(6.4) s=XX′
In this expression X represents the raw data matrix, X' its transpose, and s the resulting covariance or correlation matrix. Given this relation, the degree to which the new factor loadings for a PCA or a factor analysis accounts for the structure of the original covariance/correlation matrix can be determined by multiplying the eigenvector and/or factor loading matrix by its transpose. If we do this for the two-axis PCA and factor analysis results for our trilobite data, the results might surprise you (Table 6).
| PCA | Factor Analysis | |||||
|---|---|---|---|---|---|---|
| Original Correlation Matrix | Original Correlation Matrix | |||||
| BL (x1) | GL (x2) | GW (x3) | BL (x1) | GL (x2) | GW (x3) | |
| BL (x1) | 1.000 | 0.895 | 0.859 | 1.000 | 0.895 | 0.859 |
| GL (x2) | 0.895 | 1.000 | 0.909 | 0.895 | 1.000 | 0.909 |
| GW (x3) | 0.859 | 0.909 | 1.000 | 0.895 | 0.909 | 1.000 |
| Reproduced Correlation Matrix | Reproduced Correlation Matrix | |||||
| BL (x1) | 0.901 | 0.252 | -0.157 | 0.993 | 0.916 | 0.848 |
| GL (x2) | 0.253 | 0.352 | 0.405 | 0.916 | 0.945 | 0.942 |
| GW (x3) | -0.157 | 0.405 | 0.747 | 0.848 | 0.942 | 0.981 |
Notice that reproduced correlations numerically closest to the original correlations for the PCA result (0.901, 0.747) are located along the trace of the correlation matrix. This is because the purpose of PCA is to minimize deviation along this dimension of the matrix. There is also one negative value in the PCA reproduced correlation matrix, which is a bit at odds with the all-positive correlations exhibited by the raw correlation matrix. This is a somewhat spurious by-product of the small number of variables used in this example. It would not be there if all three PCA axes were used to determine the reproduced correlation matrix and probably not be there if the number of variables and/or sample size was larger. Nevertheless, it is a good reminder that such artefacts can creep into a PCA result, especially if PCA is being used in the sense of a factor analysis. The scaling operation we used to estimate the factor loadings probably seemed somewhat trivial when you read about it above. But look at the result in terms of its ability to reproduce the original correlation matrix. In this case the two scaled factors were able to achieve a much closer approximation of the off-diagonal elements of the original correlation, while the accuracy of the diagonal elements has, to some extent, been reduced. If there were more data and/or variables in our example, this discrepancy between the PCA and factor analysis results would be even more pronounced.
Once these factor equations have been determined, they can be used to project the original data into the feature space formed by the two factor vectors. Like the scaling operation, this is a bit more involved a computation in factor analysis than in PCA. The reason is that the data matrix (X) contains a component of variation that coincides with the common factor structure (= the F-values in equation 6.2, also called latent variables) and a component that is unique to each object (= the e-values in equation 6.2). Multiplying the raw data by the factor loading matrix-as is done in classical PCA-means the common and unique components of variation are confounded. Fortunately, it's an easy matter to normalize the loading matrix for this unique component of variation in the data by normalizing the data matrix for the residual component of variation in the covariance/correlation matrix. One can do this either by inverting the covariance/correlation matrix itself...
(6.5) ˆX=Xs−1F
… or by inverting the product of the transposed and normal factor loading matrices (F'F)...
(6.6) ˆX=XF(F′F)−1
The resulting factor scores (ˆX) may then be tabulated, interpreted, and/or plotted in the normal manner (Table 7, Fig, 2).
| Genus | Factor 1 | Factor 2 |
|---|---|---|
| Acaste | -1.056 | 0.993 |
| Balizoma | -1.162 | 0.110 |
| Calymene | 0.530 | -0.889 |
| Ceraurus | -0.924 | -0.333 |
| Cheirurus | 0.168 | 1.737 |
| Cybantyx | 0.234 | 0.495 |
| Cybeloides | -0.580 | 0.168 |
| Dalmanites | -0.356 | -0.854 |
| Delphion | -0.427 | 1.437 |
| Ormathops | -1.078 | 0.319 |
| Phacopdina | -0.607 | 0.594 |
| Phacops | -0.502 | 0.433 |
| Placopoaria | 0.016 | -0.314 |
| Pricyclopyge | 0.771 | 1.491 |
| Ptychoparia | 0.650 | -2.753 |
| Rhenops | 1.342 | 0.048 |
| Sphaerexochus | -0.963 | -0.661 |
| Toxochasmops | 0.299 | -0.158 |
| Trimerus | 2.921 | 0.031 |
| Zacanthoides | 0.723 | 0.091 |
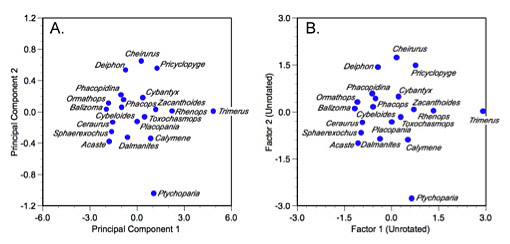
Figure 2. Plot of trilobite genus scores on the first two principal components (A) and two common factors (B) of the correlation matrix. Note similarity of the ordination despite strong axis scaling differences that arise as a result of scaling the factor axis lengths and normalization for the unique aspects of the factor solution.
Now, compare a plot of these scores to a plot of the first two PCA axes calculated from the trilobite correlation matrix. Although most features of the ordination have not changed substantively (e.g., Trimerus and Ptychoparia are still unambiguous outliers, Pricyclopyge and Acaste lie on opposite sides of the distribution), the detail has changed a bit. This is, once again, a reflection of the fundamental differences between PCA and factor analysis. The PCA ordination reflects the original geometry of the sample to a much greater extent than the factor analysis ordination. The PCA result is an optimized portrayal of variance across the sample re-expressed along two mutually independent axes. The factor analysis result, on the other hand, represents a truer picture of inter-correlations among taxa that have been optimized along two factor axes. Note also the difference in the scaling of the PCA and factor axes. The PCA ordination represents a more accurate picture of the scaling differences among taxa in the sample (albeit from standardized data). The factor analysis ordination represents a variance-reduced space that is not portraying those aspects of the raw data idiosyncratic to individual specimens. That component of variance was normalized out when computing the factor scores.
Of course, part of the reason these ordination results are very similar is that we're not working with much data. As alluded to before, more variables and/or more specimens in the dataset would likely accentuate the differences between PCA and factor analysis. Morphological data are also fairly well-behaved in this respect. Regardless, same data, different results-especially in terms of the factor loadings and the structure of the reproduced correlation matrix-because the data analysis methods are trying to do very different things. As usual, it's up to the data analyst to decide which approach best suits the needs of any particular investigation.
We've now completed a basic presentation of geological factor analysis as applied to our trilobite example, except for one final topic; axis rotation. In the comparatively simple world of classical PCA, the axes are the axes, are the axes. What you get out of the (plus a bit of matrix multiplication) is what you see on the graph. Not so with factor analysis. As if all the different ways in which to do a factor analysis (see below for references) weren't enough, someone had to come along and invent axis rotation!
The intention of axis rotation is straight-forward and perfectly reasonable. Say we have a two-factor solution to a more complicated problem than our trilobite example. When we plot the factor loadings their orientations usually look like those in Figure 3A.
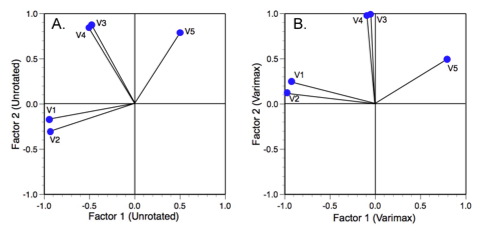
Figure 3. Unrotated (A) and varimax rotated (B) factor axis solutions to an analysis of 7 variables measured on 20 random boxes (see Davis 2002).
Obviously these variables form subsets that, for morphological data, may reflect either necessary or interesting linkages between variation in different regions of the form (e.g., developmental modules). For these data there are three groups of variables. Most people familiar with PCA or factor analysis would have no trouble interpreting this result. However, when many axes are involved the interpretation can become more difficult. One way to simplify this problem is to rigidly rotate the axes about the origin of the coordinate system until they achieved a position of maximum alignment with different factor axes; something like Figure 3B.
Because the rotation has been rigid, the orientations of the variables relative to one another have not changed. This means the geometry of the analysis itself hasn't changed. The same groups of variables are present and they differ from one another by exactly the same amount. The only thing that has changed is the orientation of the vector swarm relative to the underlying factor-axis coordinate system. That's now been changed in such a way as to make the relations between the variable axes and the factor axes easier to understand and interpret. After rotation variables 1 and 2 are maximally aligned (subject to the rigid rotation constraint) with factor axis 1 whereas variables 3 and 4 are aligned with factor axis 2. Variable 5 occupies an intermediate position along both axes as a result of the fact that it does not exhibit strong covariance with any other variable.
A variety of axis rotation schemes are available for use in factor analysis to achieve this structural simplification. Indeed, there seem to be as many ways to specify an axis rotation scheme as there are to skin the proverbial cat. This is felt by many to be one of the downsides to factor analysis insofar as there are as many solutions to a rotated factor analysis problem as there are axis rotation methods and no good guide as to which rotation method is best in which context. Two generalized approaches to this problem exist, the 'orthogonal' (= rigid rotation) approach and the 'oblique' approach. Orthogonal rotation methods are the most popular. The most popular orthogonal method-and the one used in this example-is the varimax rotation scheme. This axis-rotation strategy only adjusts the component of variance common to the specified factor structure and does so iteratively, two axes at a time, until the improvement in the factor loading structure drops below some previously specified cut-off value.
As indicated by the name, orthogonal methods preserve the right-angle orientation of the underlying factor axis system. In other words, the variable vectors are rigidly rotated about an unchanging set of orthogonal factor axes. This having been said, there are still a large number of ways within which an orthogonal rotation can be accomplished. Mostly these methods use different weighting schemes to summarize the appropriateness of the rotation. Aside from varimax, normal varimax, quartimax, and equimax are all orthogonal rotation schemes.
Oblique rotation goes one step further and relaxes the constraint of orthogonality on the factor axes (that is essentially derived from eigenanalysis). Under this protocol extreme variable vectors within the swarm become synonymous (or near synonymous) with individual factor axes (loadings = 1.0) and the entire space deformed such that all axes lie at various angles from one another. While this approach achieves perhaps the ultimate in simplifying the overall structure of the variable system, it does so by sacrificing the natural analogy to normal physical spaces and can make the production of accurate graphics difficult. Oblique rotations can be useful, but they are not for the faint-hearted. As for names, olbimin, quatrimin, biquartimin, orthoblique and promax are all oblique rotation methods.
Let's finish by applying the varimax rotation to our trilobite factor results. Table 8 shows the equations of the unrotated and varimax-rotated factor loadings.
| Variables | F1 | F2 |
|---|---|---|
| Factor Loadings (Unrotated) | ||
| Body Length (x1) | 0.954 | 0.285 |
| Glabella Length (x2) | 0.972 | -0.041 |
| Glabella Width (x3) | 0.959 | -0.242 |
| Factor Loadings (Varimax Rotated) | ||
| Body Length (x1) | 0.501 | -0.861 |
| Glabella Length (x2) | 0.737 | -0.636 |
| Glabella Width (x3) | 0.866 | -0.480 |
Figure 4 shows our three variable axes in their unrotated (A) and varimax rotated (B) positions.
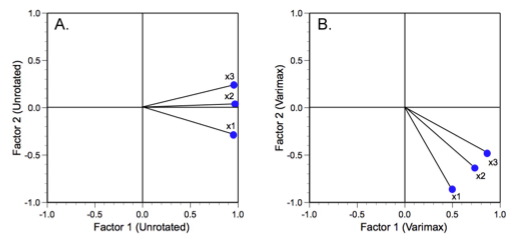
Figure 4. Alternative positioning of factor analysis reference axes for the trilobite dataset.
There are two ways to look at these tables and plots. One can either regard the factor axis coordinate system as fixed and the factor loading vectors as having rotated about the coordinate system origin (this is the sense you get from the figure), or you can regard the factor loading vectors as fixed and the factor axis system as having rotated about the common vector origin5. Either way the result is the same.
Because the original variables are all highly correlated with on another (see Table 6), the unrotated factor axes all exhibit low angles relative to one another. This is also typical for morphological data. The two glabellar measures lie at a smaller angle to one another than either do with respect to the body length variable. These relations are preserved during varimax rotation. But note how the rotation does make the geometric relations between the variables clearer in Table 8. This is important because the interpretation of these relations would normally be gauged on the basis of the factor loading table. After varimax rotation it is much clearer how close the orientations of these variables are on the dominant F1 axis. The linkage between the glabellar measurements is also present on the subdominant F2 axis, though it is a little harder to see because, after rotation, there are no longer any distinctions in the loading signs. Nevertheless, these distinctions are still there in terms of differences in the F2 loading magnitudes.
Because the varimax is a rigid, orthogonal rotation, interpretation of the factor scores for the set of genera is not enhanced in the same way as interpretation of the factor loadings (Fig. 5). For this example in particular, the somewhat arcuate distribution of the genera against the two common factors is largely unchanged, leading to the factor score plot being little more than a rigid two-dimensional rotation of the unrotated scores. Had more variables been involved some adjustment of the relative positions of individual taxa within the subspace defined by the first two factor axes might have been noticed.
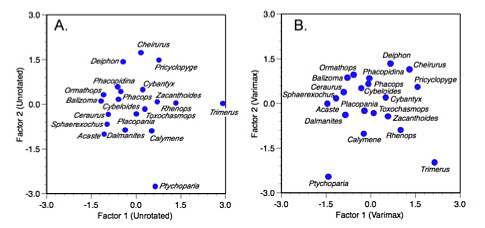
Figure 5. Unrotated (A) and varimax rotated (B) factor score plots for the trilobite dataset.
Factor analysis has a long and distinguished history in palaeontology. Imbrie and Kipp (1971) based their transfer-function approach to palaeoclimate modelling on factor analysis. The late Stephen Jay Gould-who was building an innovative career as a quantitative paleontological data analyst before he became 'side tracked' by punctuated equilibrium-used factor analysis extensively for a variety of morphological analyses (e.g., Gould 1967, Gould and Garwood 1969, Gould and Littlejohn 1973). Jack Sepkoski learned his factor analysis from Gould while at Harvard as Gould's student and then went on to employ the method in his studies of Phanerozoic biodiversity (e.g., Sepkoski 1981). Indeed, Sepkoski's three evolutionary faunas were originally recognized on the basis of a loading-pattern analysis on a three-factor model of his diversity data.
From a computational point-of-view factor analysis is not problematic. Nevertheless, owing to ongoing confusion about its relation to PCA and owing to the sheer number of approaches to factor analysis available, it has not been well implemented in a number of standard data analysis packages. For the most part, these packages treat PCA and factor analysis as more-or-less variants of each other. This is understandable to some extent in that there is a genuinely large group of methods and techniques that can be applied to either PCA or factor analysis results. For example, axis rotation can be applied to the results of a classical PCA as easily as to the results of a factor analysis. The advantages of this operation will be largely the same in both cases. Similarly, the operation that scales the lengths of the eigenvectors by the eigenvalues can also be applied within the context of a PCA as easily as in a factor analysis. Most mathematical discussions of PCA include presentation of these variations. However, for me the single computation that marks out the boundary between factor analysis and PCA is the manner in which the factor scores are calculated (equations 6.5 or 6.6). Ironically, this is the aspect of 'factor analysis' that has received comparatively little attention by those seeking to extend or vary the method. Then again, perhaps that's telling us something. This normalizing computation that lies at the heart of the factor score calculation signals a basic change in the manner in which one is treating the raw data. Under the classic PCA approach, such a normalization would not be considered because the data are not regarded as having to be 'corrected' for any intrinsic aspect of their variation. There is no error term in the basic PCA model (see (PalaeoMath 101: Principal Components Analysis [Eigenanalysis & Regression 5], Equation 5.1). There is-irreducibly-an error term in the factor analysis model (see equations 6.1 and 6.2). This changes everything in terms of the concepts and computations involved in factor analysis.
Therefore, if you run across a computer package (and you will) that uses anything other than the raw eigenvector matrix to compute the PC scores, it's likely that package is confusing the distinction between classical PCA and factor analysis in favor of the latter. Similarly, though less frequently, you might find a package that computes for factor scores directly from the eigenvector matrix. In this case such a package would be confusing a factor analysis with PCA. Fortunately, the computations involved in performing both analyses are not difficult and, if you're careful, can be readily carried out in MS-Excel (see example worksheet) augmented by a macro routine to extract the eigenvalues and eigenvectors of a symmetric matrix (e.g., PopTools). Alternatively, you can easily write your own PCA and/or factor analysis programmes in various mathematics programmes like Mathematica or MathCAD. If you must use the routines provided in dedicated, commercial software, please be careful to understand what these programmes are actually doing to your data and how their results are being obtained. Otherwise you are very likely to make incorrect, or incomplete, interpretations.
References
DAVIS, J. C. 2002. Statistics and data analysis in geology (third edition). John Wiley and Sons, New York, 638 pp.
HAMMER, Ø., and D. HARPER. 2006 (actually 2005). Paleontological data analysis. Blackwell Publishing, Oxford, 351 pp.
GOULD, S. J. 1967. Evolutionary patterns in pelycosaurian reptiles: a factor analytic study. Evolution, 21, 385-401.
--- 1981. The mismeasure of man. W. W. Norton & Company, 352.
--- and R. A. GARWOOD. 1969. Levels of integration in mammalian dentitions: an analysis of correlations in Nesophontes micrus (Insectivora) and Oryzomys couesi (Rodentia). Evolution, 23, 276-300
--- and J. Littlejohn. 1973. Factor analysis of caseid pelycosaurs. Journal of Paleontology, 47, 886-891.
IMBRIE, J., and N. G. KIPP. 1971. A new micropaleontological method for quantitative paleoclimatology: Application to a Pleistocene Caribbean core, 72-181. In TUREKIAN, K. K., (ed.) The Late Cenozoic Glacial Ages. Yale University Press, New Haven, 606 pp.
JACKSON, J. E. 1991. A user's guide to principal components. John Wiley & Sons, New York 592 pp.
JOLLIFFE, I. T. 2002. Principal component analysis (second edition). Springer-Verlag, New York, 516 pp.
JÖRESKOG, K. G., KLOVAN, J. E., and REYMENT, R. A. 1976. Geological factor analysis. Elsevier, Amsterdam, 178 pp.
MANLEY, B. F. J. 1994. Multivariate statistical methods: a primer. Chapman & Hall, Bury, St. Edmonds, 215 pp.
SEPKOSKI, J. J., Jr. 1981. A factor analytic description of the Phanerozoic marine fossil record. Paleobiology, 7, 736-53.
SWAN, A. R. H., and M. Sandilands. 1995. Introduction to geological data analysis. Blackwell Science, Oxford, 446 pp./p>
Addendum to PalaeoMath 101 - Part 5: PCA, Eigenanalysis & Regression IV
A correspondent who wishes to remain anonymous recently pointed out that, in my preliminary discussion of allometry toward the end of the last essay I may have inadvertently confused careful readers by seeming to imply that the loadings on an isometric PCA vector must be equal. This indeed, is the case, but only once the data have been log-transformed first, as per the standard linear transform of the allometric equation ( y = xm is the same as log y = m log x). As promised last time, an entire column devoted to the analysis of allometry will be is scheduled for the near future. Many thanks to my anonymous friend for bringing this to my attention.
Footnotes
1 This seemingly straight-forward interpretation of Spearman's work later became highly controversial when estimates of a person's general intelligence were used to direct or limit their life opportunities and when the culturally biased character of many standard 'intelligence' tests was recognized (see Gould 1981 for a review).
2 The paperback copy of this book lists 2006 as the publication year though the Blackwells website lists 1 Oct. 2005 as the publication date.
3 This is called a Scree Test because the plot resembles a profile across an alluvial fan the upper part of which is composed of the large, angular blocks rocks with a higher angle of repose that mountaineers and geologists call 'scree'.
4 A transposed matrix is one in which the rows and columns of the original matrix have been interchanged. In MS-Excel a tool for transposing matrixes will be found in the 'Paste Special' dialog of the 'Edit' pull-down menu.
5 In this particular analysis the new axes would form an angle of 45° with the unrotated factor axes.
