8. Minding your Rs and Qs II
Written by Norm MacLeod - The Natural History Museum, London, UK (email: n.macleod@nhm.ac.uk). This article first appeared in the Nº 62 edition of Palaeontology Newsletter.
Part 2 - Correspondence Analysis
Last time we took a look at how we might want to approach the quantitative analysis of measured ‘objects’ (e.g., specimens, localities, samples in a section or core) as opposed to variables, and drew a useful distinction between R-mode and Q-mode analyses. No doubt you noticed over the past several essays that, despite our geometric approach to the analysis of any data matrix, we’re really interested in both quantities. You may have even asked yourself, “isn’t there anything that does both?”. There is, and we’ll spend this essay discussing one of the most popular ways to do so. Along the way we’ll compare and contrast this new method to some of our old friends and (hopefully) gain a bit deeper insight into what multivariate analysis is all about.
Correspondence analysis (CA) grew from the ground prepared by Pearson’s (1901) early work on what came to be known as principal components analysis (PCA) and Spearman’s (1904) work on the original factor analysis (FA) model. Both these approaches were concerned with the decomposition of similarity matrices into components or factors that represented a more complex, underlying structure. Their success implied that it might be possible to do the same thing with any table of data. By ‘any table of data’ I don’t mean a data table of any size or shape. That situation can be handled by PCA and FA as you already know them. Rather, this statement refers more to different types of data.
Since CA derives much of its power from being able to handle different types of data, a brief digression is called for here. We touched on this last time in our discussion of Q-mode similarity coefficients. There, we said different similarity coefficients were needed because a variety of data can be collected from objects. Now it’s time to come to grips with this topic in a more systematic manner.
Quantitative data come in four basic types: nominal, ordinal, interval, and ratio. The difference between these is the manner in which they incorporate the concept of scale.
- Nominal data are simply number names for different, mutually exclusive groups of objects (e.g., 1 = dog, 2 = cat, 3 = horse). These data contain no scale information and are most frequently represented as contingency tables.
- Ordinal data represent observations that can be ranked with reference to some external scale (e.g., 0 = small, 1 = medium, 2 = large). These data embody information about the rank order of the categories, but nothing else.
- Interval data have a true scale, in the sense that the magnitudes of the numbers express important information. The classic example of an interval-scale variable is temperature expressed as °F or °C. In both those scales the difference between 2.4° and 1.1° is the same as the difference between 3.7° and 2.4°, but the zero point of both scales is set arbitrarily.
- Ratio data have equivalent steps in magnitude and true zero points. Lengths are typical examples of ratio-scale variables.
The regression and component-factor analysis methods we’ve discussed previously have, for the most part, assumed interval or ratio-scale data. Of course, our trilobite data matrix is composed entirely of ratio-scale variables. Correspondence analysis was originally developed to provide an eigenanalysis-based means for analyzing nominal and ordinal scale variables, though it can, just as easily, analyze interval or ratio-scale variables and/or data matrices that mix different variable types. Not only that, it scales these data such that relations between objects and variables can be graphed on the same ordination plot and used to refine the interpretation of those data. All in all it’s a neat trick, and there’s little wonder you are seeing more correspondence analyses appearing in the palaeontological literature.
We’ll begin our presentation with a classical CA of ordinal-scale data.
| Genus | Paralic Shale | Shoal Lmstn. | Upper Lmstn. | Mid. Lmstn. | Phant. Lmstn. | Org. Siltstn. | Black Shale | Row Total |
|---|---|---|---|---|---|---|---|---|
| Acaste | 8 | 5 | 3 | 10 | 4 | 5 | 1 | 36 |
| Balizoma | 6 | 6 | 5 | 10 | 2 | 3 | 1 | 33 |
| Calymene | 8 | 7 | 7 | 13 | 2 | 2 | 1 | 40 |
| Ceraurus | 10 | 1 | 1 | 10 | 10 | 11 | 4 | 47 |
| Cheirurus | 10 | 9 | 1 | 14 | 13 | 19 | 2 | 68 |
| Cybantyx | 9 | 3 | 1 | 9 | 8 | 10 | 3 | 43 |
| Cybeloides | 5 | 4 | 1 | 7 | 6 | 9 | 3 | 35 |
| Dalmanites | 6 | 4 | 1 | 7 | 5 | 7 | 2 | 32 |
| Deiphon | 9 | 7 | 3 | 12 | 4 | 5 | 1 | 41 |
| Ormathops | 9 | 5 | 1 | 10 | 8 | 10 | 2 | 45 |
| Phacopidina | 5 | 3 | 2 | 6 | 3 | 4 | 2 | 25 |
| Phacops | 9 | 7 | 3 | 12 | 5 | 6 | 1 | 43 |
| Placoparia | 6 | 6 | 2 | 8 | 5 | 7 | 2 | 36 |
| Pricyclopyge | 3 | 1 | 0 | 3 | 8 | 9 | 8 | 32 |
| Ptychoparia | 10 | 9 | 2 | 14 | 9 | 13 | 2 | 59 |
| Rhenops | 6 | 1 | 1 | 6 | 5 | 5 | 3 | 27 |
| Sphaerexochus | 7 | 2 | 2 | 8 | 4 | 5 | 2 | 30 |
| Toxochasmops | 7 | 5 | 4 | 10 | 3 | 3 | 1 | 33 |
| Trimerus | 2 | 2 | 2 | 3 | 2 | 2 | 4 | 17 |
| Zacanthoides | 4 | 4 | 1 | 5 | 10 | 14 | 5 | 43 |
| Column Total | 139 | 91 | 43 | 177 | 116 | 149 | 50 | 765 |
Here we are looking at a hypothetical distribution of trilobite genera among different environmental facies representing a peritidal-bathyal transect. This is a typical contingency table. The numbers are occurrence frequencies of the different genera among the environments. Our problem is to infer the character of faunal similarity relations among environments (R-mode analysis of the matrix columns) and the character of environmental-preference similarities among the genera (Q-mode analyses of the matrix rows), simultaneously. Since there are seven variables and twenty objects, a premium will also be placed on dimensionality reduction so we can summarize the greatest amount of information in the lowest number of composite variables. In the end we want a single plot, or set of plots, that will tell us everything we need to know about this system of variables and objects.
Our first problem is the fact that the sums of the matrix rows and the columns are numbers of characteristically different magnitudes. This is the typical situation. The methods we’ve discussed previously (PCA, FA, PCoord) finesse this issue because they focus on analysing only one type of similarity relation, either that among variables (PCA, R-mode FA) or among objects (Q-mode FA, PCoord). Correspondence analysis considers the matrix from both points of view. Accordingly, this discrepancy must be corrected. Otherwise, the scale of the resulting composite variables will not be comparable.
In order to render the scales comparable we divide each element of the matrix by the grand sum of the matrix, which is the sum of the sums of rows (or the sum of the sums of columns).
(8.1)
bij=xijn∑i=1p∑j=1xij
Dividing a frequency observation by the total number of times the observation has occurred provides an estimate of its proportion of the total occurrence pattern. This proportion is also an estimate of the probability of finding the observation at that locality, horizon, genus, etc. Accordingly, the matrix resulting from this scaling operation is an expression of the joint probabilities genera will be found in specific environments and specific environments will contain genera.
In Table 2, the row totals (Bi∙) represent the marginal probabilities of each genus occurring in any environment. Similarly the column totals (B∙j) represent the marginal probabilities that specific environments will contain any trilobites. Naturally, both groups of marginal probabilities sum to 1.000.
Now comes the first complex part. If the trilobite faunas of two environments are similar we would expect to find similar patterns of variation in the proportion of trilobite genera in each column. If the environments differ in terms of their trilobite fauna, the joint probabilities should be different. This holds for the rows too. Thus, we should be able to come up with an index to express the similarities between rows and columns.
| Genus | Paralic Shale | Shoal Lmstn. | Upper Lmstn. | Mid. Lmstn. | Phant. Lmstn. | Org. Siltstn. | Black Shale | Bi∙ |
|---|---|---|---|---|---|---|---|---|
| Acaste | 0.010 | 0.007 | 0.004 | 0.013 | 0.005 | 0.007 | 0.001 | 0.047 |
| Balizoma | 0.008 | 0.008 | 0.007 | 0.013 | 0.003 | 0.004 | 0.001 | 0.043 |
| Calymene | 0.010 | 0.009 | 0.009 | 0.017 | 0.003 | 0.003 | 0.001 | 0.052 |
| Ceraurus | 0.013 | 0.001 | 0.001 | 0.013 | 0.013 | 0.014 | 0.005 | 0.061 |
| Cheirurus | 0.013 | 0.012 | 0.001 | 0.018 | 0.017 | 0.025 | 0.003 | 0.089 |
| Cybantyx | 0.012 | 0.004 | 0.001 | 0.012 | 0.010 | 0.013 | 0.004 | 0.056 |
| Cybeloides | 0.007 | 0.005 | 0.001 | 0.009 | 0.008 | 0.012 | 0.004 | 0.046 |
| Dalmanites | 0.008 | 0.005 | 0.001 | 0.009 | 0.007 | 0.009 | 0.003 | 0.042 |
| Deiphon | 0.012 | 0.009 | 0.004 | 0.016 | 0.005 | 0.007 | 0.001 | 0.054 |
| Ormathops | 0.012 | 0.007 | 0.001 | 0.013 | 0.010 | 0.013 | 0.003 | 0.059 |
| Phacopidina | 0.007 | 0.004 | 0.003 | 0.008 | 0.004 | 0.005 | 0.003 | 0.033 |
| Phacops | 0.012 | 0.009 | 0.004 | 0.016 | 0.007 | 0.008 | 0.001 | 0.056 |
| Placoparia | 0.008 | 0.008 | 0.003 | 0.010 | 0.007 | 0.009 | 0.003 | 0.047 |
| Pricyclopyge | 0.004 | 0.001 | 0.000 | 0.004 | 0.010 | 0.012 | 0.010 | 0.042 |
| Ptychoparia | 0.013 | 0.012 | 0.003 | 0.018 | 0.012 | 0.017 | 0.003 | 0.077 |
| Rhenops | 0.008 | 0.001 | 0.001 | 0.008 | 0.007 | 0.007 | 0.004 | 0.035 |
| Sphaerexochus | 0.009 | 0.003 | 0.003 | 0.010 | 0.005 | 0.007 | 0.003 | 0.039 |
| Toxochasmops | 0.009 | 0.007 | 0.005 | 0.013 | 0.004 | 0.004 | 0.001 | 0.043 |
| Trimerus | 0.003 | 0.003 | 0.003 | 0.004 | 0.003 | 0.003 | 0.005 | 0.022 |
| Zacanthoides | 0.005 | 0.005 | 0.001 | 0.007 | 0.013 | 0.018 | 0.007 | 0.056 |
| B∙j | 0.182 | 0.119 | 0.056 | 0.231 | 0.152 | 0.195 | 0.065 | 1.000 |
Fortunately, there is such an index. The derivation is a tad complicated and I won’t go into it in detail. Good—though somewhat mathematical—discussions of this index can be found in the references listed at the end of this column. Effectively what the mathematics does is scale the transformed data (B) by the reciprocal of the square root of the marginal row and column probabilities (B−1/2r and B−1/2c, respectively). In matrix notation the equation is as follows.
(8.2)
H=B−1/2rBB−1/2c
In order to make this calculation, the Br -1/2 and Bc -1/2 matrices need to be arranged so that the marginal probabilities are located in the matrix diagonals with all off-diagonal values set to 0.0 (see the PalaeoMath 101: R&Qs II worksheet for details of the calculations). This calculation estimates the conditional probabilities specific genera will be found in specific environments and vice versa. Another way of thinking about this calculation is that it’s scaling, or weighting, the column values by the reciprocal of the row sums (and so forming a weighted average) and scaling the row values by the reciprocal of the column sums. This, in turn, leads to the other name for CA, ‘reciprocal averaging’ or ‘reciprocal averaged PCA’. As a by-product, this weighted averaging also helps equalize the scales within the rows and between columns, but it does not enforce equal scaling (as does correlation-based PCA or R-mode FA).
The H matrix of conditional probabilities for our trilobite frequency analysis is listed below.
| Genus | Paralic Shale | Shoal Lmstn. | Upper Lmstn. | Mid. Lmstn. | Phant. Lmstn. | Org. Siltstn. | Black Shale | Row Total |
|---|---|---|---|---|---|---|---|---|
| Acaste | 0.113 | 0.087 | 0.076 | 0.125 | 0.062 | 0.068 | 0.024 | 0.556 |
| Balizoma | 0.089 | 0.109 | 0.133 | 0.131 | 0.032 | 0.043 | 0.025 | 0.561 |
| Calymene | 0.107 | 0.116 | 0.169 | 0.154 | 0.029 | 0.026 | 0.022 | 0.624 |
| Ceraurus | 0.124 | 0.015 | 0.022 | 0.110 | 0.135 | 0.131 | 0.083 | 0.620 |
| Cheirurus | 0.103 | 0.114 | 0.018 | 0.128 | 0.146 | 0.189 | 0.034 | 0.733 |
| Cybantyx | 0.116 | 0.048 | 0.023 | 0.103 | 0.113 | 0.125 | 0.065 | 0.594 |
| Cybeloides | 0.072 | 0.071 | 0.026 | 0.089 | 0.094 | 0.125 | 0.072 | 0.548 |
| Dalmanites | 0.090 | 0.074 | 0.027 | 0.093 | 0.082 | 0.101 | 0.050 | 0.517 |
| Deiphon | 0.119 | 0.115 | 0.071 | 0.141 | 0.058 | 0.064 | 0.022 | 0.590 |
| Ormathops | 0.114 | 0.078 | 0.023 | 0.112 | 0.111 | 0.122 | 0.042 | 0.602 |
| Phacopidina | 0.085 | 0.063 | 0.061 | 0.090 | 0.056 | 0.066 | 0.057 | 0.477 |
| Phacops | 0.116 | 0.112 | 0.070 | 0.138 | 0.071 | 0.075 | 0.022 | 0.603 |
| Placoparia | 0.085 | 0.105 | 0.051 | 0.100 | 0.077 | 0.096 | 0.047 | 0.561 |
| Pricyclopyge | 0.045 | 0.019 | 0.000 | 0.040 | 0.131 | 0.130 | 0.200 | 0.565 |
| Ptychoparia | 0.110 | 0.123 | 0.040 | 0.137 | 0.109 | 0.139 | 0.037 | 0.694 |
| Rhenops | 0.098 | 0.020 | 0.029 | 0.087 | 0.089 | 0.079 | 0.082 | 0.484 |
| Sphaerexochus | 0.108 | 0.038 | 0.056 | 0.110 | 0.068 | 0.075 | 0.052 | 0.506 |
| Toxochasmops | 0.103 | 0.091 | 0.106 | 0.131 | 0.048 | 0.043 | 0.025 | 0.548 |
| Trimerus | 0.041 | 0.051 | 0.074 | 0.055 | 0.045 | 0.040 | 0.137 | 0.443 |
| Zacanthoides | 0.052 | 0.064 | 0.023 | 0.057 | 0.142 | 0.175 | 0.108 | 0.621 |
| Column Total | 1.891 | 1.514 | 1.098 | 2.130 | 1.700 | 1.910 | 1.203 | 11.446 |
Now most of the hard work is done. As before, genera (rows) and/or environments (columns) that are similar to one another should exhibit similar patterns of values. Drawing on analogy with previous multivariate methods, we now need to summarize this between-rows and betweencolumns similarity with a numerical index. We can do this in a couple of different ways. The method most similar to PCA, FA, and PCoord is to calculate the covariance between columns of the H matrix. Because of the probability calculations we have performed, this quantity (d) represents the product of two X2 values, and is sometimes referred to as a X2 ‘distance’. Once you have obtained the H matrix the easiest way to calculate the matrix of X2 distances (D) is as follows.
(8.3)
D=H′H
In this equation H′ is the transpose of the H matrix and the matrix multiplication is equivalent to calculating the sum of squares and cross products between all pairs of columns. Since we had previously designated the columns of X to contain our variables, D is analogous to an R-mode distance matrix. The D matrix for our trilobite frequency data set is listed below.
| Paralic Shale | Shoal Lmstn. | Upper Lmstn. | Mid. Lmstn. | Phant. Lmstn. | Org. Siltstn. | Black Shale | |
|---|---|---|---|---|---|---|---|
| Paralic Shale | 0.191 | 0.148 | 0.107 | 0.214 | 0.159 | 0.179 | 0.097 |
| Shoal Lmstn. | 0.148 | 0.138 | 0.098 | 0.176 | 0.120 | 0.140 | 0.069 |
| Upper Lmstn. | 0.107 | 0.098 | 0.094 | 0.131 | 0.068 | 0.075 | 0.048 |
| Mid. Lmstn. | 0.214 | 0.176 | 0.131 | 0.245 | 0.173 | 0.196 | 0.104 |
| Phant. Lmstn. | 0.159 | 0.120 | 0.068 | 0.173 | 0.170 | 0.193 | 0.115 |
| Organic. Siltstn. | 0.179 | 0.140 | 0.075 | 0.196 | 0.193 | 0.222 | 0.126 |
| Black Shale | 0.097 | 0.069 | 0.048 | 0.104 | 0.115 | 0.126 | 0.111 |
Note this matrix is symmetric about its diagonal or trace. An eigenanalysis of the D matrix yields the following eigenvalues, which express the character of between-facies biotic similarity relations
| Eigenvalue | % Variation | Cum. % Variation | |
|---|---|---|---|
| 1 | 1.000 | 85.412 | 85.412 |
| 2 | 0.117 | 10.022 | 95.435 |
| 3 | 0.036 | 3.090 | 98.524 |
| 4 | 0.014 | 1.159 | 99.683 |
| 5 | 0.003 | 0.270 | 99.953 |
| 6 | 0.000 | 0.026 | 99.979 |
| 7 | 0.000 | 0.021 | 100.000 |
In CA the first eigenvalue is usually 1.000. Obviously the first three eigenvalues represent the overwhelming majority of the variation. Arguably the first two do, but you’ll see why I’m going to interpret three in a moment. Eigenvector 7 is going to be 0.0 (save for rounding error) because we’ve scaled the data and so removed a component of variation. Eigenvector 6 exists (0.0003) but is too small to show up in a report to three decimal places.
These eigenvalues correspond to the eigenvectors of the D matrix, which are what we will use to produce an ordination plot of the similarity relations between environments. To do so these values are first scaled by the square roots of the eigenvalues in a manner identical to the one we used in PCoord Analysis (see previous PalaeoMath 101 column: Minding your Rs and Qs). Then, in order to make it possible to plot both the R-mode and Q-mode loadings in the same coordinate space, these scaled values are scaled again by the square roots of the Q-mode conditional probabilities (= column sums) of the B matrix, as follows.
(8.4)
Ar−scaled=B1/2cAr
The results of these calculations are shown below.
| Environments | R-Mode Eigenvectors | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| Paralic Shale | 0.426 | 0.166 | 0.102 |
| Shoal Lmstn. | 0.345 | 0.310 | 0.127 |
| Upper Lmstn. | 0.237 | 0.491 | -0.479 |
| Mid. Lmstn. | 0.481 | 0.328 | 0.062 |
| Phantom Lmstn. | 0.389 | -0.381 | 0.139 |
| Organic Siltstn. | 0.441 | -0.429 | 0.324 |
| Black Shale | 0.256 | -0.447 | -0.784 |
| Singular Value-Scaled Eigenvectors | |||
| 1 | 2 | 3 | |
| Paralic Shale | 0.426 | 0.057 | 0.019 |
| Shoal Lmstn. | 0.345 | 0.106 | 0.024 |
| Upper Lmstn. | 0.237 | 0.168 | -0.091 |
| Mid. Lmstn. | 0.481 | 0.112 | 0.012 |
| Phantom Lmstn. | 0.389 | -0.130 | 0.026 |
| Organic Siltstn. | 0.441 | -0.147 | 0.062 |
| Black Shale | 0.256 | -0.153 | -0.149 |
| Cond. Probability (Q)-Scaled Eigenvectors | |||
| 1 | 2 | 3 | |
| Paralic Shale | 0.182 | 0.024 | 0.008 |
| Shoal Lmstn. | 0.119 | 0.037 | 0.008 |
| Upper Lmstn. | 0.056 | 0.040 | -0.022 |
| Mid. Lmstn. | 0.231 | 0.054 | 0.006 |
| Phantom Lmstn. | 0.152 | -0.051 | 0.010 |
| Organic Siltstn. | 0.195 | -0.065 | 0.027 |
| Black Shale | 0.065 | -0.039 | -0.038 |
The resulting plots of the similarity structure among environments for the first three correspondence axes (Fig. 1) present the data at the bottom of Table 6 graphically.
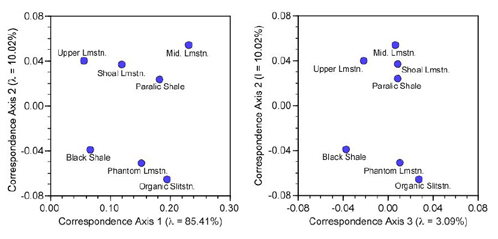
Figure 1. Scaled R-mode loadings on the first three trilobite frequency data correspondence axes.
These ordination plots are deceptively simple. As always, care needs to be taken with their interpretation. The clearest substructure among environments is the separation of shallower facies (Paralic Shale, Shoal Limestone, Middle Limestone, Upper Limestone) from the deeperwater facies (Phantom Limestone, Organic Siltstone, Black Shale). However, that separation occurs along the second correspondence axis, which represents only 10 percent of the overall variation (Table 5). The environment (facies) points are spread out along the first CA axis with no obvious clustering. What aspect of the original data matrix X is this pattern expressing?
When in doubt, return to the basis matrix (in this case the R-mode X2 ‘distance’ matrix, Table 4) and the original data (Table 1). Everything there is to see in the data should be visible there, especially if your eye has been clued in by seeing the ordination of R-mode loadings. The Black Shale and Upper Limestone facies plot low along CA-Axis 1. Inspection of Table 4 shows the ‘biotic distance’ between these facies is the lowest in the table. They should be close to one another along the predominant eigenvector. The pattern at one end of CA-Axis 1 should then be compared with that at the other end: the Organic Siltstone and Middle Limestone facies. Both are located at a relatively large distance from the Black Shale and Upper Limestone facies, and this is borne out by their distances from these facies in Table 4. This gives us confidence that the plot is a faithful picture of relations within the R-mode X2 ‘distance’ matrix and encourages us to look further, to the original data. Take a look at Table 1 now and see whether you can find the pattern responsible for the distribution of facies along CA-Axis 1.
Did you find it? It’s a bit subtle but it’s there. If you didn’t see it don’t give up (and don’t be lazy). Go back and look for it. No pain no gain and all that. Here’s a hint: Think about the bottom line of any matrix-based data analysis. Of course, I’m stalling a bit here so the answer is buried in the text. If you’re going to undertake multivariate analyses you need to develop a skill at looking for and finding the geometric patterns you see in the ordination plots within tables of numbers. But if you took that ‘bottom line’ bit to heart you now know that the distribution of points along CA-Axis 1 represents a measure of the relative frequency of trilobite occurrence in each of the facies. In retrospect, this is perfectly understandable. Those ‘bottom line’ numbers summarize a dominant pattern among facies created by considering the data across all trilobite genera.
Many CA practitioners will tell you the best practice is to interpret only the correspondence axes that have eigenvalues less than 1.000 and term the first axis a ‘trivial’ or ‘nuisance’ factor (see Manley, 1994). After all, we already extracted that information during our scaling operations (it’s the Bc matrix). This sort of CA-Axis 1 result doesn’t show up in every CA analysis, but it’s not uncommon. Some describe it as a trivial or ‘nuisance’ factor since it really doesn’t tell us much about the relation between genera and facies we didn’t already know without having dragged all the complex mathematical machinery of a full-blown correspondence analysis out of the closet. Still, ‘trivial’ and ‘nuisance’ are relative terms. It all depends on what you’re looking for.
We now have interpretations of correspondence axes 1 and 2. What about CA-Axis 3? As with CA-Axis 1, we see the Black Shale and Upper Limestone facies form a group on the low end of that axis while the other four facies cluster together at the high end. Is the interpretation the same? Not quite. The ordination of facies along CA-Axis 1 is not clustered to the same degree and represents a pattern strictly controlled by the trilobite relative occurrence frequency. Not so with CA-Axis 3. Inspection of Tables 1 and 4 doesn’t reveal an obvious pattern and, owing to the small amount of variance expressed on this axis, we really wouldn’t expect them to. But there must be a reason for it.
Here is where the power of CA reveals itself. What we need is an explanation of the ordination pattern of facies along CA-Axis 3 in terms of the pattern of trilobite occurrences. In effect, we need to relate patterns of between-columns variation to patterns of between-rows variation. That’s what CA does, and does more effectively than any of the methods we’ve discussed thus far. So how do we perform the Q-mode analysis in the context of CA? Best to go through the same set of calculations we did before, but this time focus on comparisons between rows rather than columns.
A couple of convenient mathematical theorems make this Q-mode analysis a snap. The first and most important of these is the Ekhart-Young Theorem which we’ve already met informally in the guise of Gower’s (1966) proof that a PCoord analysis of a Q-mode squared Euclidean distance matrix is an exact mirror, or ‘dual’, of the covariance-based R-Mode PCA for the same data (see previous PalaeoMath 101 column: Minding your Rs and Qs). Ekhart and Young theorized that any real matrix X is equivalent to the product of three matrices, V, W, and U such that …
(8.5)
X=VWU′
Matrix V is the set of Q-mode eigenvectors. Matrix U′ is the transpose of the R-mode eigenvectors. Matrix W is the diagonalized matrix of ‘singular values’ that are equivalent to the square roots of the eigenvalues. Note here that all those times I’ve been asking you to multiply or divide matrix values by the square root of the eigenvalues in the previous PCoord analysis and above, I’ve really been asking you to make use of the data matrix’s singular values. Goulub and Reinsch (1971) devised a method for finding these matrices directly and their method (with improvements) is now called singular value decomposition or SVD. The important result of the Ekhart and Young Theorem we need to make use of now is that, for real matrices such as the one we’ve transformed our trilobite frequency data into, the R-mode and Q-mode eigenvalues are the same (because the singular values of these matrices are the same). That means we don’t have to recalculate the Q-mode eigenanalysis. We’ve already determined the eigenvalues of both analyses (see Table 5).
Since we already have the W matrix we can easily use that to calculate the Q-mode CA loadings we need using the following equations.
(8.6)
Aq=HArW−1
(8.7)
Aq−scaled=B1/2rAq
This is equivalent to scaling each of the Q-mode eigenvector loadings by the corresponding singular value and the scaling by the R-mode conditional probabilities (= square roots of the row sums of the B-matrix). Results of this calculation for the first three correspondence axes (= eigenvectors) are shown below.
| Genus | Q-Mode Correspondence Axis Loadings | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| Acaste | 0.047 | 0.013 | 0.001 |
| Balizoma | 0.043 | 0.024 | -0.007 |
| Calymene | 0.052 | 0.035 | -0.012 |
| Ceraurus | 0.061 | -0.018 | 0.002 |
| Cheirurus | 0.089 | -0.014 | 0.023 |
| Cybantyx | 0.056 | -0.011 | 0.004 |
| Cybeloides | 0.046 | -0.010 | 0.001 |
| Dalmanites | 0.042 | -0.003 | 0.003 |
| Deiphon | 0.054 | 0.018 | 0.003 |
| Ormathops | 0.059 | -0.005 | 0.010 |
| Phacopidina | 0.033 | 0.003 | -0.004 |
| Phacops | 0.056 | 0.015 | 0.004 |
| Placoparia | 0.047 | 0.003 | 0.002 |
| Pricyclopyge | 0.042 | -0.035 | -0.018 |
| Ptychoparia | 0.077 | 0.001 | 0.013 |
| Rhenops | 0.035 | -0.007 | -0.004 |
| Sphaerexochus | 0.039 | 0.002 | -0.002 |
| Toxochasmops | 0.043 | 0.019 | -0.004 |
| Trimerus | 0.022 | -0.003 | -0.016 |
| Zacanthoides | 0.056 | -0.028 | -0.001 |
Plotting axes 2 and 3 in the same coordinate system as the R-mode loadings gives us the following diagram.
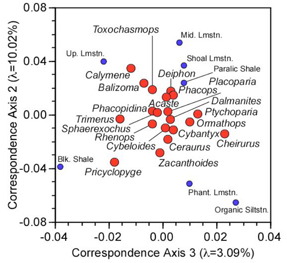
Figure 2. Q-mode loadings on the correspondence axes 2 and 3.
Comparison of figures 1 and 2 now reveals why the Black Shale and Upper Limestone facies are being pulled down along the third axis. Pricyclopyge exhibits a unique deep-water distribution and its relatively high abundance in the Black Shale facies is differentially affecting the placement of that facies. Similarly, the Upper limestone facies is being pulled down by the shallow-water occurrence pattern of Calymene and, to a lesser extent, Balizoma. Both these patterns are further reinforced by the unusual distribution of Trimerus. Note that the combined plot of the scaled R-mode and Q-mode loadings is also conveniently centred on the centroids of both datasets.
The ability of CA to handle simultaneous R-mode and Q-mode analyses in a manner that really improves the interpretation of data matrices and ordination plots is a big plus in the technique’s favour. So is its similarity to PCA and FA, both of which have proven their usefulness in many different data analysis contexts. But there is another advantage possessed by CA that needs brief discussion: flexibility.
Recall that PCA is used to conduct R-mode analyses of data matrices composed of real numbers with no missing values. R-mode factor analysis can be used in the same manner, but is built on a different mathematical model than PCA. Principal Coordinates–Q-mode factor analysis can handle a variety of different data types, but only if you select an appropriate similarity/ dissimilarity index. Correspondence analysis combines the best parts of all these methods and, as a bonus, can be used to analyse almost any type of data. In the example above we used it to analyse occurrence frequencies. Because of the scaling calculations inherent in CA, this would be possible even if a large number of cells in the X matrix were occupied by zeros (= no observations or missing data). But while CA was originally developed to handle the case of contingency-table data, it is not restricted to analyzing nominal or ordinal data. It can handle interval and ratio data just as easily. To demonstrate this, here’s a CA ordination of the original trilobite body and glabellar length data we’ve used throughout this series.
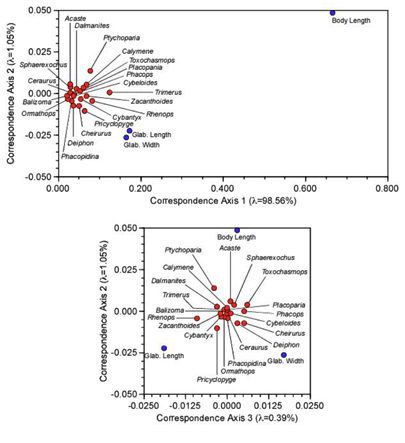
Figure 3. R-mode (hollow circles) and Q-mode (solid discs) correspondence axis scores for axes 1 and 2 (upper) and 2 and 3 (lower) of the trilobite body and glabellar size data
Comparing these plots to Figure 7 of the PCA column (Newsletter vol. 59) shows that, with minor changes in relative point spacing (brought about as a result of the scaling calculations), the ordinations are very similar, with all outlying points in comparable relative positions. In that previous column recall we had to jump back and forth between the table of eigenvectors (shown just above Table 5 of the PCA column) and the plots in order to develop a sense of the geometric meaning of the PCA subspaces. We still need the eigenvectors to interpret the CA subspaces. But it’s much easier and intuitive to develop these interpretations when a representation of the eigenvector ‘positions’ can be graphed on the same diagram.
The method I’ve illustrated above scales the results in terms of the B matrix. One can easily preserve the scale of the original X matrix by conducting all weighting operations using the original X matrix along with the row and column sums from that matrix. The singular values, eigenvalues, and eigenvectors will be the same, but the magnitudes of the H matrix, and D matrix, along with the various row matrices, column matrices, and eigenvector loading (= score) matrices, will be larger. The relative placement of points within the ordination diagrams should remain unchanged.
I appreciate this has been the most complex mathematical presentation of the series (thus far) and both thank and congratulate you if you’ve stuck with me to this point. As you can probably imagine there’s much more to the mathematics of CA than I’ve presented here. What I’ve tried to do is give you enough maths to understand what CA is about, how to interpret CA results, how CA relates to the methods we’ve discussed previously. The PalaeoMath 101 spreadsheet for this column contains a complete worked example of the trilobite frequency analysis. Look to that to clarify details of the calculations.
Correspondence analysis is a newer data analysis method and is being included in more highend multivariate statistical analysis packages these days (e.g., SPSS, SAS, Multitab, Statistica, GenStat). Not everyone has access to such packages, however, and it is expensive to acquire personal copies. Among the less expensive commercial software packages, XLStat (http://www.xlstat.com/en/home/) has a good implementation, as does CANOCO (http://www.pri.wur.nl/uk/products/canoco/). With a bit of practice and access to public-domain Excel routines like PopTools (http://www.cse.csiro.au/poptools/), though, you can easily make up an Excel spreadsheet that will perform simple CA analyses.
Sometimes you will see reference to a variant of CA termed ‘detrended correspondence analysis’ or DCA. This is a standard CA to which a post-processing step has been added in order to remove the possibility of generating ordinations that look like a parabola or a wave (also called the ‘arch effect’, horseshoe effect’, ‘Guttman effect’). Such results are usually obtained when analysing datasets in which there is strong gradient. Those who perform Q-mode analyses of any sort on a routine basis run into such results sooner or later. They are especially common in ecological analyses because one often runs into gradient-like structures in ecological data. Despite looking rather strange when you first encounter one, there’s nothing wrong with an analysis that produces such a result. All it really means is that an important aspect of your data’s variation is organized or patterned in a non-linear manner.
‘Detrending’ such plots sounds like a grand thing to do. Usually it’s not. The most popular detrending algorithm arbitrarily subdivides the range of the data along one CA axis (usually CAAxis 1) into a set of n bins and centres the data falling into each bin about 0.0. This removes the trend and ‘linearizes’ the data. But other than responding to an aesthetic desire to remove nonlinearities from the CA scores, there seems little justification either for applying this method of post hoc data ‘correction’ or preferring it to other conceivable methods (e.g., applying a curvilinear regression or spline function and representing the data along the CA-Axis 1 as residuals from the regression or spline axis). Indeed, such ad hoc manipulations can destroy aspects of the data’s pattern that are important for its correct interpretation (see Watenberg et al. 1987 for a critical review). The safest course of action is always to try to stay as close to the raw data as possible.
My advice is not to correct any analytic result for what amounts to aesthetic reasons. If you find a horseshoe in your results it’s telling you something about your data (presence of a gradient or some other source of non-linear signal). Use that information to understand how the pattern relates to your hypothesis test. Good discussions of, and further references to, the horseshoe effect can be found in Greenacre (1989), Reyment (1991) and Reyment and Joreskog (1993). Early and ecological practitioners of CA—and those influenced by them—often advocate detrending (e.g., Pielou 1984, Hammer and Harper 2006). More recent commentators, especially those concerned with applications in the geological sciences, have been decidedly more sceptical as to the technique’s value. Certainly the application of such ‘corrections’ to data in which there is no non-linear trend (see examples above) is entirely unnecessary and indefensible.
The methods on which modern approaches to CA are built are among the most powerful in the entire field of linear algebra. We’ll encounter them again when we discuss how patterns of variation in one set of variables can be related to those on other sets of variables. Looking back though, CA is perhaps best understood as a generalization of PCA. Anything you can do with PCA you can do with CA. The main difference between the methods is that PCA allows you to choose whether to retain the original scale of the data (unstandardized, covariance-based PCA) whereas CA, of course, requires the data be normalized to ‘correct for’ scaling differences. The ability of CA to handle more different types of data is a product of its attention to scaling issues, and a clear advantage in terms of the number of different types of data analysis situations it can cope with. It is possible to scale PCA and FA results to portray both eigenvector loadings and the scores of objects on the same PCA/FA axis, using methods developed in the context of CA. I can present those variations on PCA/FA analyses if there’s any interest.
Finally, a word about where CA leads us. There is a school of thought in multivariate data analysis that focuses on dimensionality reduction of complex numerical data and the production of graphs that express ‘relations’ between ‘entities’ in a low-dimensional space. This is the field of multidimensional scaling. Most often the purpose of these methods is simply to produce a picture of the data with little or no interest in the parameters of the data that control the graphical representation. The methods of PCA, PCoord, and CA are members of this family of data analysis techniques, and can be collectively referred to as classical approaches to the multidimensional scaling problem. There are other approaches (e.g., non-metric multidimensional scaling) that are even more generalized than CA. What I’ve tried to do here is show that the classical scaling methods can not only be used to produce the picture of your data. They can also help you understand it. That’s the ultimate plus in my book.
References
DAVIS, J. C. 2002. Statistics and data analysis in geology (third edition). John Wiley and Sons, New York. 638 pp.
GOLUB, G. H. and REINSCH, C. 1971. Singular value decomposition and least squares solutions, 134–151. In WILKINSON, J. H. and REINSCH, C., eds). Linear algebra: computer methods for mathematical computation, v. 2. Springer-Verlag, Berlin.
GOWER, J. C. 1966. Some distance properties of latent roots and vectors used in multivariate analysis. Biometrika, 53, 588–589.
GREENACRE, M. J. 1984. Theory and applications of correspondence analysis. Academic Press, London. 364 pp.
HAMMER, Ø. and HARPER, D. 2006 (actually 2005). Paleontological data analysis. Blackwell Publishing, Oxford, UK. 351 pp.
JACKSON, J. E. 1991. A user’s guide to principal components. John Wiley & Sons, New York. 592 pp.
MANLEY, B. F. J. 1994. Multivariate statistical methods: a primer. Chapman & Hall, Bury St. Edmonds, Suffolk. 215 pp.
PEARSON, K. 1901. On lines and planes of closest fit to a system of points in space. Philosophical Magazine, 2, 557–572.
PIELOU, E. C. 1984. The interpretation of ecological data. John Wiley & Sons, New York. 263 pp. REYMENT, R. A. 1991. Multidimensional paleobiology. Pergamon Press, Oxford. 539 pp.
REYMENT, R. A. and JÖRESKOG, K. G. 1993. Applied factor analysis in the natural sciences. Cambridge University Press, Cambridge. 371 pp.
SPEARMAN, C. 1904. ‘General intelligence’, objectively determined and measured. American Journal of Psychology, 15, 201–293.
WARTENBERG, D., FERSON, S., and ROHLF, F. J. 1987. Putting things in order: a critique of detrended correspondence analysis. American Naturalist, 129, 434–448.
