1. Introduction, the R language and plotting data
During a recent conversation with the Newsletter editor, Al McGowan, about the possibility of writing a column on programming with R I was reminded about a question I was once asked during a job interview. When asked what, if anything, I would have done differently during my PhD I replied that I would have learned how to code in R from the outset. This skill has had a huge effect on my research, allowing me to perform a much wider range of analyses as well as allowing me to develop methods that suit my exact needs. Also, having all the code I need for data processing, analysis and outputting of figures in a single package saves the need for moving data between multiple platforms that may require the data to be in different formats.
There has been a growing movement in recent years to widen opportunities to learn the basics of computer programming, with websites such as www.code.org and www.codeacademy.com devoted to just that. I appreciate that to the novice the art of programming in any language may appear daunting. However for those currently reading this and thinking ‘but I can’t code’, trust me with a little bit of work you most certainly can.
My aim with these articles is not to provide a compendium of all the functions and capabilities of R, but to introduce the basics of programming and statistical analyses, and to introduce some of the most commonly used packages within R. Throughout these articles I have provided a number of examples that can be run directly in R, all of which are highlighted, for instance:
Some Example R-codeFinally, all the code and data files required to reproduce graphs/analyses will be placed on the Palaeontological Association website in due course.
Why use R?
Since its release in the mid-1990s R has become one of the most commonly used statistical environments. Within the field of palaeontology, R has become a common tool for a wide range of analyses including: trait evolution (Hunt, 2007; Sookias et al., 2012; Young et al., 2011); rates of morphological evolution (Lloyd et al., 2012); the quality of the rock record (Benson and Mannion, 2012) and geometric morphometrics (Arbour and Brown, 2014). It has several advantages that make it a valuable statistical package for academics at least. Firstly and importantly it is open source, freely available and supported on UNIX, Mac and Windows operating systems. Secondly, the graphics package within R allows for the creation of publication-quality vector figures that can be quickly and easily changed without the need for fiddling around with other graphics software (e.g. Illustrator). Finally, one of the most useful features of R is the package system, allowing users to create libraries of functions for specific purposes ranging from plotting functions to more complex analytical toolkits (currently there are over 5,000 registered packages). Several packages are available that are of particular use to palaeontologists, and I will focus on these in greater detail in later articles. One extremely useful package is APE (Analysis of Phylogenetic Evolution) (Paradis et al., 2006), which is designed for the manipulation and analysis of phylogenetic data (both morphological and molecular).
Installation and the R console
R can be easily downloaded from the CRAN website (Comprehensive R Archive Network), at www.r-project.org. From here you will need to follow the ‘download R’ link and choose a mirror site (e.g. www.stats.bris.as.uk/R), then you can choose the appropriate version for your operating system. The current version is R v.3.0.2 although, unless otherwise stated, the code I provide here will work just as well on previous versions.
You won’t need to install any packages to get started; R already comes with a wide range of functions related to arithmetic calculations, statistical tests and graphics. When you first open it you will be met with the R console (Figure 1). You’ll see the command prompt (>); this is where you will enter your instructions to R. For example if you type 2+3 after the prompt then press [Enter], R recognizes this as a mathematical equation and will return the number 5 on the next line (Figure 1.1).
When working in R it is good practice not to write all your code directly into the R console but to use a text editor such as the one provided in R (File>New script). This has several advantages, not least in backing up your work just in case your computer were to crash. Also it allows you to run your entire program at once, which is especially useful with large analyses. Another piece of good coding advice is to make use of the hash-tag (#); this tells R to ignore anything placed after it. It is wise to use the hash-tag to comment your code explaining what the purpose of that line is. This helps when coming back to a project after a long period of time or to help another user understand what you were doing.
Before we begin with the basics of programming, syntax and plotting there is one other important feature of R I want to introduce, and that is the help system. Every R package and function has an associated help page that provides a description, list of all the options, and example code. If you want to see the help page for the function plot type either help(plot) or ?plot. Should you want a more general search for all plotting functions, type ??plot. If you want you can run just the example code provided; try typing in example(plot) or example(log).
Syntax and data types Now is the best time to introduce the terminology associated with different types of data and data manipulation that I will be using throughout this series. Simply speaking, any data that you will use in your analyses must be given a name; this is called a variable. There are several different modes of data that can be stored as variables including numeric (e.g. 1, 10), character (e.g. “a”, “hello”) or logical (e.g. TRUE or FALSE). Assigning information as a variable is commonly done using the <- symbol. The simplest form of data is known as a scalar, that contains only one value; for example if you wish to create the variable x that contains the number 4 you would type:
x <- 4If you then type x R will return the number 4. It is important to note that R variables are case sensitive, so x is different from X. The second data type is known as a vector, which is a variable that contains more than one scalar of the same mode (e.g. all numerical, or all characters). You can create these in multiple ways such as simply concatenating the values using the concatenate function c:
y <- c(11,12,13,14,15,16,17,18,19,20)Or you can use a series function to create a sequence of numbers, such as separating the extremes of the range you want by a colon (:):
y <- 11:20Or through using the function seq that creates a sequence of numbers that increase at a rate specified by the user through the argument by:
y <- seq(from=11,to=20,by=1)Finally, a matrix is a multidimensional variable made up of both rows and columns, so you can think of a vector as a one-dimensional matrix with just one row. In order to create an empty matrix you use the function matrix, and to fill it you use the argument data:
z <- matrix(ncol=2,nrow=2,data=c(1:4))If you now call z you will get the following:
[,1] [,2]
[1,] 1 3
[2,] 2 4You will have noticed that there are two different kinds of brackets used by R; square [ ] and rounded ( ). These have distinct uses: the rounded ones are used in functions while the square brackets are used to define the location of different elements within vectors, matrices etc. Because scalars and vectors have only one dimension, only one number is required between the brackets to locate a particular value(s). Returning to vector y that we created earlier, to return just the second element you would type:
y[2]
[1] 12If you wanted multiple elements such as the 1st and 5th you can use the concatenate (c) function from before and type:
y[c(1,5)]
[1] 11 15You can also put logical commands between the square brackets if you wanted to return only values that matched a particular condition, such as those that were greater than 15:
y[y>15]
[1] 16 17 18 19 20Or to be more specific:
y[y > 15 & y<18]
[1] 16 17Because matrices have two dimensions (containing both rows and columns), a comma is used to differentiate between the value for rows and columns respectively. You can think of these numbers as map grid coordinates with the rows as the northings and columns as eastings. If you call z then you can see that the values for the rows come first (e.g. [1,] and [2,]) and the columns come second (e.g. [,1] and [,2]). Using one number for either the row or the column will return all values for that row; for example z[1,] will return the numbers 1 and 3 whereas if you specify both the row and column R will return only the value of one cell, so in our example z[1,2] will return the number 3.
Introduction to functions
Most of the work in R is done with functions. These are pieces of independent code that take in one or more data files either to transform (e.g. calculate the mean) or to be used in an analysis (e.g. Principal Components Analysis, PCA), the results of which are returned to the user. Within functions are a series of options or arguments that are used for specific purposes related to that function. The help files for every function will tell you what the default settings are for the arguments (under ‘Usage’) as well as providing an explanation of the options allowed in each case. For example in the function sort the argument decreasing can be set to either TRUE or FALSE, with FALSE being the default.
v <- c(10,1,15,3,20,9,12)
sort(v)
[1] 1 3 9 10 12 15 20
sort(v,decreasing=TRUE)
[1] 20 15 12 10 9 3 1Vector calculations
Now that you’ve created a number of small datasets you can start to perform some basic calculations. Taking the vector v as an example, any calculation you want to perform (e.g. multiplication, *; division, /; addition, +; or subtraction, -) will be performed on each element individually. For example:
v*2
[1] 20 2 30 6 40 18 24
v/2
[1] 5.0 0.5 7.5 1.5 10 4.5 6.0There are a great many functions that apply to the entire vector, providing descriptive statistical values on that dataset. Some examples of these are shown in Table 1.1.
| Function | Description |
|---|---|
min(y) | The smallest value in y |
max(y) | The largest value in y |
sum(y) | The sum of all values in y |
sort(y) | Sorting values of y, use option descending=TRUE to reverse the order |
range(y) | Returns the largest and smallest values of y |
mean(y) | The average of all values in y |
median(y) | The median value of vector y |
quantile(y) | Returns the quartile values for vector y |
cumsum(y) | Returns the cumulative sum of all values in the vector |
sd(y) | The standard deviation of vector y |
sum(v)
[1] 70
range(v)
[1] 1 20
mean(v)
[1] 10Example datasets
For this article the data file extrinsic.txt is taken from the supplementary information of Mayhew et al. (2012) and contains measures of diversity, temperature and rock area measurements for the Palaeozoic. The second example dataset, named asaphidae.txt, contains a series of measurements taken from twenty-one trilobite genera of the Family Asaphidae (Bell and Braddy, 2012). In addition to these the file Number 1 – Introduction.R contains the relevant code for Figures 1.2-1.3.
| File Name | Size | Download |
|---|---|---|
asaphidae.txt | 198kb | |
extrinsic.txt | 14kb |
Basics of plotting
The function plot is one of the most useful in the R repertoire, although there are many other plotting functions, many of which are for specific analyses/data types (e.g. b). This function also provides an excellent way-in for new users to understand how functions work and the effect of the many arguments such as those built into plot.
Before you can plot or analyse your data they must be loaded into the R environment. A useful first step is to change the working directory to the folder where your data files are located. This means that files can be quickly loaded without the need to type out the entire location. Also this is the location where R will save any data or figures you have created, keeping everything in the same place. The working directory is set using the function setwd as below, and you can find out where it is currently set to by typing getwd( ). The result will look something like the examples below on my computers, but will reflect your own computer’s file directory.
setwd("/Users/markbell/Newsletter") # For Mac users setwd("C:/Users/markbell/Newsletter") # For PC users
Next you can load in the file extrinsic.txt using the function read.table; the argument header if set to TRUE tells R that the first row of data should be considered as the column names.
extrinsic<-read.table(file="extrinsic.txt",header=TRUE)Now that the data have been read into R you can start to explore and plot them. Try calling the first column using extrinsic[,1] or the first row using extrinsic[1,]. The file extrinsic has column names that you can see if you type in names(extrinsic), and you can use the column names instead of the row/column numbers. So to get the first column you can also use extrinsic[,"Age"].
The function plot only requires a vector of information, a list of values, to create a plot. Figure 1.2a represents a basic plot using plot(extrinsic[,"Rock.area_europe"]), plotting the values of the column ‘Rock.area_europe’ against the index, or the position of each value in the vector; simply put, it plots the values in order. Plotting two variables requires both an explanatory variable (x-axis) and a response variable (y-axis); Figure 1.2b, shows the same data plotted against the column "Age" – the geological age in millions of years.
plot(extrinsic[,"Age"],extrinsic[,"Rock.area_europe"])There are a large number of arguments available to plot that can be used to control the size, shape, colour of everything from the individual points to the tick marks on the axes (Figure 1.2c,d). Table 1.2 provides a list of useful arguments and examples of how to apply them (see the ‘Graphical Parameters’ section of help(par) for a more comprehensive list). You can add another dataset on top of the first using points or lines (Figure 1.2d).
plot(extrinsic[,"Age"],extrinsic[,"Rock.area_europe"],type="l")
points(extrinsic[,"Age"],extrinsic[,"Rock.area_australia"],type-"l",col="red")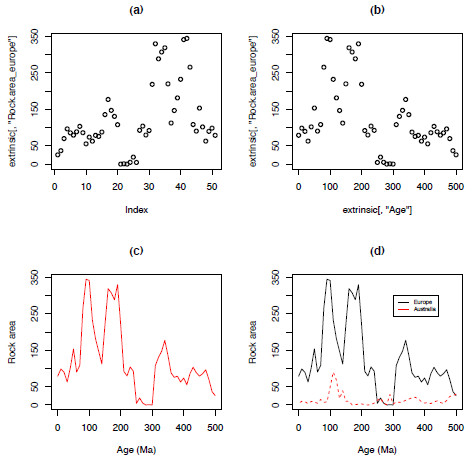
| Argument | Result | Example of usage |
|---|---|---|
pch | The type of the plotted points | plot(extrinsic[,1],extrinsic[,2],pch=19) |
cex | The size of the individual points | plot(extrinsic[,1],extrinsic[,2],cex=2) |
type | The kind of plot: "l" – lines, "p" – points, "b" – both | plot(extrinsic[,1],extrinsic[,2],type="l") |
lwd | The width of any plotted lines | plot(extrinsic[,1],extrinsic[,2],type="l",lwd=2) |
lty | The type of line: 1 – solid, 2 – dashed, 3 – dotted | plot(extrinsic[,1],extrinsic[,2],type="l",lty=3) |
xlab, ylab | The label of the x, y axes | plot(extrinsic[,1],extrinsic[,2],xlab="Age(Ma)") |
xlim, ylim | The range of the x, y axes | plot(extrinsic[,1],extrinsic[,2],xlim=c(100,200)) |
col | The colour of the points of lines | plot(extrinsic[,1],extrinsic[,2],col="red") |
log | Changes the axes to a log scale | plot(extrinsic[,1],extrinsic[,2],log="y") |
main | Text to use as a header for the plot | plot(extrinsic[,1],extrinsic[,2],main="Hello world") |
In addition to bivariant plots you may wish to compare the distribution of two or more samples of your data; this can be done either statistically or visually. For now I will focus on the two visual methods of examining the distribution of your data: histograms and box plots. Histograms display the distribution of a sample of the number of counts (frequency) of the sample between discrete intervals. Box plots (or box and whisker plots) show the same distribution using a box that represents the first and third quartiles or the 25th and 75th percentiles of the data with a horizontal line representing the median or the 50th percentile. The whiskers refer to the vertical line joining the upper and lower limits of the distribution.
Using the dataset asaphidae.txt the distribution of the body-size of one of more genera can be shown using both a histogram (Figure 1.3a) and box plots (Figure 1.3b).
asaphidae<-read.table("asaphidae.txt",header=T)
hist(asaphidae[,"Isotelus"],xlab="isotelus") # for histograms
boxplot(asaphidae[,"Isotelus"],asaphidae[,"Asaphus"],names=c("Isotelus","Asaphus"), xlab="Genus",log="y") # for boxplots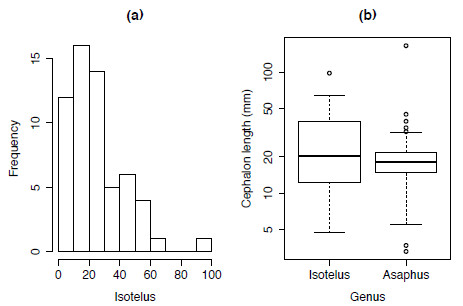
Figure 1.3. Plotting the body-size distribution of trilobite genera using (a) histograms and (b) boxplots.
A quick note on your own data
Sometimes, for the first time user, one of most annoying issues can be getting R to read in your data without returning an error. These errors can range from not finding the file of that name (in that case check the working directory is correct) to the data containing either blank cells or not having as many values in a row as there are headers. Here are a few tips to help you read in your data successfully.
If you have a table of observations you want to analyse in R the best way is to save the table as a tab-delimited file (.txt) as R can’t read in an excel file directly for example. However, it should be noted that R does not like blank cells either. One way around this is to enter NA (short for not available) into any blank cells – which will be read as empty by R. Another way to deal with the problem of gaps in your data is to save the file as a comma-separated file (.csv) and load it in using the function read.csv.
In addition you will see that in the file extrinsic.txt no column headers contain any spaces, but – for example – "Sepkoski_p" instead of "Sepkoski p". In the second example R would read "Sepkoski" and "p" as two different column names and return an error asking why there are not enough values to fill all the columns it thinks your data has.
Saving your work
Finally, at the end of a productive day of coding you will want to save your code, results, figures or the entire workspace. While you can save the workspace or the contents of the plotting window from the menu system (File > Save workspace) I personally find it more useful to save figures from the command line, outputting files as the code is running.
Using write.table will save a data file as a .txt file to your working directory. If you want you can save only the columns you have been working with. The argument sep determines how the values are separated in the file; e.g. "\t" specifies tab-spaced.
extrinsic_new <- extrinsic[,c("Age","IQS")]
write.table(extrinsic_new,file="new data.txt",sep="\t")For figures, the function pdf will save all figures you create between pdf() and dev.off() into the one file.
pdf(file="plot.pdf")
plot(extrinsic[,"Age"],extrinsic[,"IQS"],type="o",col="red")
plot(extrinsic[,"Age"],extrinsic[,"SQS"],type="o",col="blue")
dev.off()Finally, saving your entire workspace, using the function save.image, will allow you to continue exactly where you left off with all your data files, variables and functions already loaded into the R environment.
save.image("workspace.RData")Summary
By the end of this article I hope that you will be able to load and plot your data in R as well as run some of the most basic of statistical functions. Next time I plan to go over the basics of writing your own functions as well as an introduction to some of the statistical tests available in R.
References
- ARBOUR, J. H. and BROWN, C. M., 2014. Incomplete specimens in geometric morphometric analyses: Methods in Ecology and Evolution, 5, 16–26.
- BELL, M. A. and BRADDY, S. J., 2012. Cope’s rule in the Ordovician trilobite Family Asaphidae (Order Asaphida): patterns across multiple most parsimonious trees. Historical Biology, 24, no.3, 223–230.
- BENSON, R. B. J. and Mannion, P. D., 2012. Multi-variate models are essential for understanding vertebrate diversification in deep time. Biology Letters, 8, 127–130.
- HUNT, G., 2007. The relative importance of directional change, random walks, and stasis in the evolution of fossil lineages. Proceedings of the National Academy of Sciences of the United States of America, 104, no.47, 18404–18408.
- LLOYD, G. T., WANG, S. C. and BRUSATTE, S. L., 2012. Identifying heterogeneity in rates of morphological evolution: discrete character change in the evolution of lungfish (Sarcopterygii; Dipnoi). Evolution, 66, no.2, 330–348.
- MAYHEW, P. J., BELL, M. A., BENTON, T. G. and McGOWAN, A. J., 2012. Biodiversity tracks temperature over time. Proceedings of the National Academy of Sciences of the United States of America, 109, no.38, 15141–15145.
- PARADIS, E., CLAUDE, J. and STRIMMER, K., 2006. APE: Analysis of Phylogenetics and Evolution in R language. Bioinformatics, 20, 289–290.
- SOOKIAS, R. B., BUTLER, R. J. and BENSON, R. B. J., 2012. Rise of dinosaurs reveals major body-size transitions are driven by passive processes of trait evolution. Proceedings of the Royal Society B: Biological Sciences.
- YOUNG, M. T., BELL, M. A. and BRUSATTE, S. L., 2011. Craniofacial form and function in Metriorhynchidae (Crocodylomorpha: Thalattosuchia): modelling phenotypic evolution with maximum-likelihood methods. Biology Letters, 7, no.6, 913–916.
Futher Reading
- CRAWLEY, M. J., 2005. Statistics: an introduction using R. John Wiley and Sons. 342pp.
- FIELD, A., MILES, J. and FIELD, Z., 2012. Discovering statistics using R. SAGE publications Ltd. 992pp.
